Question

Give geometric representation of \[2y + 7 = 0\] as an equation:
1. In one variable
2. In two variable

Answer 1

Hint: Geometrically, each solution \[(x,y)\] of a linear equation in two variables, \[ax + by + c = 0\], where \[a,b,c\] are constants, corresponds to a point on the line representing the equation, and vice versa.
The one variable, we represent in graphical by a line either \[x\] or \[y\]. In this sum we use \[y\] line to represent a one variable equation or single variable equation.
The two variables, we represent in graphical by a line in \[xy - plane\].

Complete step-by-step answer:
It is given that the equation of the line is
\[2y + 7 = 0\]
We take the integer as LHS,
\[2y = - 7....\left( 1 \right)\]
Let us divided,
\[y = - \dfrac{7}{2}\]
\[y = - 3.5\]
The equation \[y = - 3.5\] is called the one variable equation or single variable equation
Hence the equation \[y = - 3.5\] an equation of one variable
That is $y$ as one variable.
Now, A linear equation with two variables is of the form \[ax + by + c = 0\] where \[a, b, c\] is constant.
To make the form, from the given equation
That is \[2y + 7 = 0\]
\[2y = - 7\]
Here, \[x - {\text{variable}}\] is missing so that, we add
\[0x + 2y = - 7\]
Taking the integer to RHS,
\[0x + 2y + 7 = 0\]
So the values are,
\[a = 0,b = 2,c = 7\]
So that the point of the given equation has \[y = - 3.5\] and \[x = 0\]
The graph can be plotted like this
\[(x,y) = (0, - 3.5)\]
We can plot these points in the Cartesian plane (two variable plane) or \[xy - plane\]
               

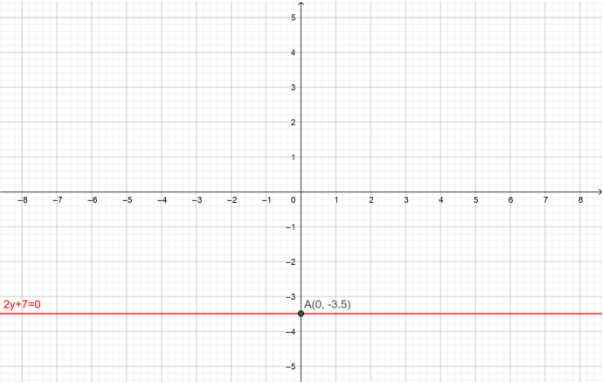
This is represented as an equation of two variables i.e. \['x'\] and \['y'\]
Hence, the given geometric equation has a one and two variable representation.

Note: The concept we use is the geometrical representation of linear equation
A one variable equation or single variable equation, a variable is a symbolic placeholder for a number we do not yet know. It’s very common to see \[x\]or \[y\]used as a variable in math problems.
A single variable equation is an equation in which there is only one variable used.
It is only a geometrical representation problem, we also solve it for graphical representation to understand the problem.