Question

Give geometric representation of \[2y + 7 = 0\] as an equation:
(i) In one variable
(ii) In two variables

Answer 1

Hint: Here we represent the given equation in geometric form on y axis in the first part and represent the equation in XY plane in the second part. Geometric representation refers to the graphical representation of the line.
(i) For the first part we have one variable y, so we find the value of y by shifting the values.
(ii) For the second part we write the equation like the general equation \[ax + by + c = 0\], where we substitute the coefficient of x as 0. We find two coordinates for two different values of y and plot the graph.

Complete step-by-step answer:
We are given the equation of line as \[2y + 7 = 0\]
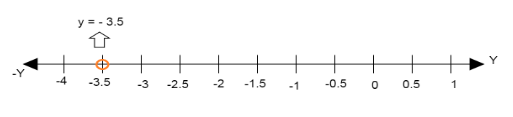
(i) Geometric representation of the line \[2y + 7 = 0\] in one variable.
Since the equation \[2y + 7 = 0\] is already in one variable i.e. y.
Therefore, we find the value of y to plot the line on the graph.
Shift the value of constant to one side of the equation.
\[ \Rightarrow 2y = - 7\]
Divide both sides by 2
\[ \Rightarrow \dfrac{{2y}}{2} = \dfrac{{ - 7}}{2}\]
Cancel the same terms from numerator and denominator.
\[ \Rightarrow y = \dfrac{{ - 7}}{2}\]
Write the value in decimal form, \[y = - 3.5\]
Therefore, we plot the point \[y = - 3.5\] on the line.

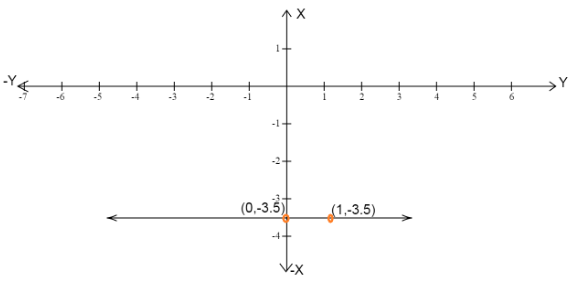
(ii) Geometric representation of the line \[2y + 7 = 0\] in two variables
We write the given equation in form of general equation in two variables \[ax + by + c = 0\]
Therefore \[2y + 7 = 0\] can be written as \[0x + 2y + 7 = 0\].
Now we substitute the values of x to get values of y.
When \[x = 0\]
\[ \Rightarrow 0 \times 0 + 2y + 7 = 0\]
Shift all constants to one side of the equation.
\[ \Rightarrow 2y = - 7\]
Divide both sides by 2
\[ \Rightarrow \dfrac{{2y}}{2} = \dfrac{{ - 7}}{2}\]
Cancel the same terms from numerator and denominator.
\[ \Rightarrow y = \dfrac{{ - 7}}{2}\]
Write the value in decimal form, \[y = - 3.5\]
Therefore, the point on the line becomes \[(0, - 3.5)\]
When \[x = 1\]
\[ \Rightarrow 0 \times 1 + 2y + 7 = 0\]
Shift all constants to one side of the equation.
\[ \Rightarrow 2y = - 7\]
Divide both sides by 2
\[ \Rightarrow \dfrac{{2y}}{2} = \dfrac{{ - 7}}{2}\]
Cancel the same terms from numerator and denominator.
\[ \Rightarrow y = \dfrac{{ - 7}}{2}\]
Write the value in decimal form, \[y = - 3.5\]
Therefore, the point on the line becomes \[(1, - 3.5)\]
Now we plot the points on the graph and join the points to form a straight line.
 

Note: Students might get confused in the second part where we have to give geometric representation in two variables as the given equation is in one variable i.e. y. Always write the second variable having the coefficient as 0. Also, while plotting the points on the graph it is always easier if you write the number in decimal form.