Question

Give a right triangle $\Delta $ ABC with $C = 90^\circ $, if a=2, c=6, how do you find b?

Answer 1

Hint: This question can be solved easily by using Pythagoras theorem. Keep in mind that the nomenclature of the triangle must not be wrong.

Formula used:
Pythagoras theorem- ${h^2} = {p^2} + {b^2}$ where ‘h’ is the hypotenuse, ‘p’ is the perpendicular and ‘b’ is the base.

Complete step by step solution:
When naming sides of the triangle, the side length opposite to the angle bears the name of the angle where the angle is represented in capital letters and the side length is represented in small letters.

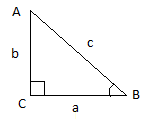
Here in this figure, $\angle C$ is $90^\circ $ and thus the side opposite to it will be the hypotenuse. Identifying the base as well as perpendicular needs a reference angle. Let’s take $\angle B$ as the reference angle. This makes side AC the perpendicular and side BC the base. Side AB is naturally the hypotenuse in this case.
Now, apply the sides in the Pythagoras formula.
$\
  {h^2} = {p^2} + {b^2} \\
\Rightarrow A{B^2} = A{C^2} + B{C^2} \\
\ $
Now we place the lengths of the sides in the same formula and get the result. We know that AB is equal to ‘c’ whose value is 6 and BC is equal to ‘a’ whose value is 2. The value of AC is b which we are supposed to find here. Putting all this in the formula,
\[\
  A{B^2} = A{C^2} + B{C^2} \\
\Rightarrow {c^2} = {b^2} + {a^2} \\
\Rightarrow {6^2} = {b^2} + {2^2} \\
\Rightarrow 36 = {b^2} + 4 \\
\Rightarrow {b^2} = 36 - 4 \\
\Rightarrow {b^2} = 32 \\
\ \]
Now that we know that \[{b^2} = 32\], a simple square root will give us the answer.
\[\
  {b^2} = 32 \\
  b = \sqrt {32} \\
   = 4\sqrt 2 \\
\ \]

Note:
Never confuse with the nomenclature. Always remember that if it is a triangle, the side length will be represented by a letter that doesn’t lie on the line joining that side to the rest of the triangle. Also, fun fact, this very diagram and the formulas used are the progenitors of all of the trigonometry.