Question

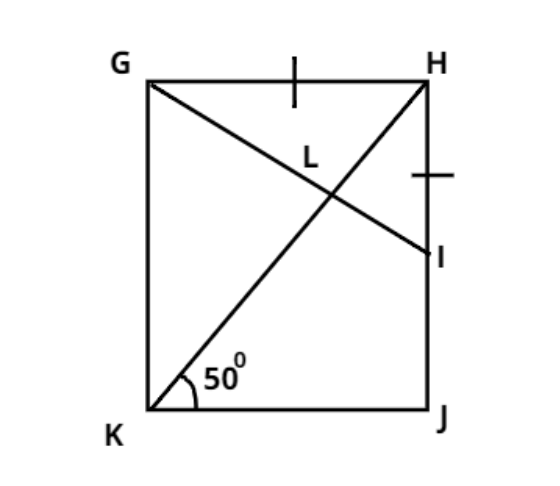
GHJK is a rectangle GH = HI and \[\angle HKJ = {50^0}\]. HLK and GLI are straight lines. Find \[\angle GLK\].

Answer 1

Hint: In this question it is given that GH = HI and \[\angle HKJ\] is also known to us. We need to find \[\angle GLK\].Use the property of the rectangle that the sides of opposite ends are perpendicular to each other at the point of meeting along with the angle sum property of a triangle to get the answer.

Complete step-by-step answer:

As we know in the rectangle all the angles are equal to${90^0}$.
$\therefore \angle GKJ = {90^0} = \angle GHJ = \angle HGK$………… (1)
And from figure it is given that $\angle HKJ = {50^0}$
Therefore $\angle GKL = \angle GKJ - \angle HKJ$
So substitute the values in above equation we have,
$ \Rightarrow \angle GKL = {90^0} - {50^0} = {40^0}$…………………….. (2)
Now from figure it is given that GH = HI
Therefore triangle GHI is an isosceles triangle.
Therefore $\angle HGI = \angle HIG$……………… (3)
And we know that in a triangle the sum of all the angles is 180 degrees.
Therefore in triangle GHI
$ \Rightarrow \angle GHI + \angle HGI + \angle HIG = {180^0}$
So from equation (1) and (3) we have
$ \Rightarrow {90^0} + \angle HGI + \angle HGI = {180^0}$
Now simplify this equation we have,
\[ \Rightarrow \angle HGI = {45^0}\]
Therefore from figure $\angle LGK = \angle HGK - \angle HGI$ so substitute the values in above equation we have,
$\angle LGK = {90^0} - {45^0} = {45^0}$……………. (4)
Now in the triangle GLK the sum of all the angles is 180 degrees.
\[ \Rightarrow \angle GLK + \angle LGK + \angle GKL = {180^0}\]
Now from equation (2) and (4) we have.
\[ \Rightarrow \angle GLK + {45^0} + {40^0} = {180^0}\]
$ \Rightarrow \angle GLK = {180^0} - {85^0} = {95^0}$
So this is the required value of the angle GLK.
Hence option (C) is correct.

Note: Whenever we face such geometry questions the key concept is simply to have the good understanding of the diagrammatic representation of the geometry given in the problem. This helps finding the specific angles and its relation with other angles with the specific triangles that we are concerned with for that particular problem. This will help getting on the right track to get the answer.