Question

From the top of the tower of height 60m, the angle of depression of the top and the bottom of a building are observed to be ${30^ \circ }$ and ${60^ \circ }$ respectively. Find the height of the building.
A) 20m
B) 60m
C) 80m
D) 40m

Answer 1

Hint:
let the height of the tower be AB=60m and building is DC=x m. let distance between the tower and building be y=BC. The angle of depression of the top and the bottom of a building are observed to be ${30^ \circ }$and ${60^ \circ }$ respectively. Then in $\Delta ABC$$\angle C = {60^ \circ }$then we can calculate the distance between the tower and building then in triangle AED ED is known and angle D is known then we can calculate the length of AE. And the height of the building is DC=BE=AB-EB.

Complete step by step solution:

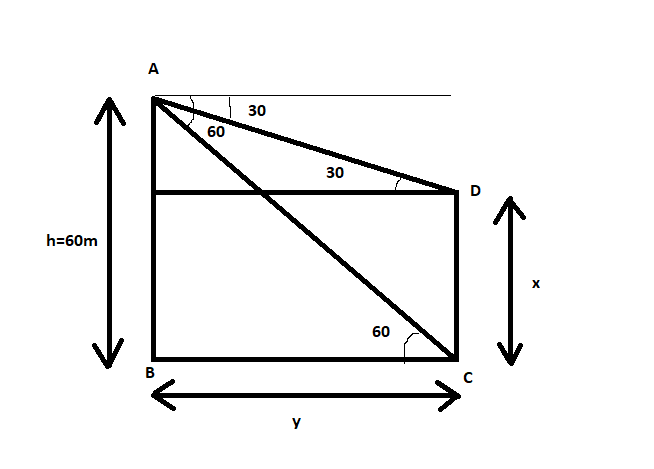
let the height of the tower be AB=60m and building is DC=x m. let distance between the tower and building be y=BC. The angle of depression of the top and the bottom of a building are observed to be ${30^ \circ }$and ${60^ \circ }$ respectively.
In $\Delta ABC$ $\angle C = {60^ \circ }$ and AB=60m we can find length of BC
$\tan C = \dfrac{{AB}}{{BC}}$
$\tan {60^ \circ } = \dfrac{{60m}}{{BC}}$
$\tan {60^ \circ } = \sqrt 3 $
Then $BC = \dfrac{{60}}{{\sqrt 3 }}m$
Now, in $\Delta ADE$$ED = BC = \dfrac{{60}}{{\sqrt 3 }}$ and $\angle D = {30^ \circ }$
Then, $\tan D = \dfrac{{AE}}{{ED}}$
$\tan {30^ \circ } = \dfrac{{AE}}{{\dfrac{{60}}{{\sqrt 3 }}}}$
$\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{AE}}{{\dfrac{{60}}{{\sqrt 3 }}}}$
$AE = \dfrac{{60}}{{\sqrt 3 }} \times \dfrac{1}{{\sqrt 3 }}m$
Therefore $AE = 20m$
$CD = BE = AB - AE$

Therefore, height of building $CD = 60m - 20m = 40m$

Note:
If a person stands and looks up at an object, the angle of elevation is the angle between the horizontal line of sight and the object. If a person stands and looks down at an object, the angle of depression is the angle between the horizontal line of sight and the object.