Question

From the top of a tower$19.6m$ high, a ball is thrown horizontally. If the line joining the point of projection to the point where it hits the ground makes an angle of $45^\circ $ with the horizontal, then the initial velocity of the ball is?
(A). $9.8m{s^{ - 1}}$
(B). $4.9m{s^{ - 1}}$
(C). $14.7m{s^{ - 1}}$
(D). $2.8m{s^{ - 1}}$

Answer 1

Hint – Start the solution by drawing a neat diagram of the motion of the ball. Use this diagram to find out how much time did the ball take to hit the ground, the distance of the point it hit the ground from the initial point. Then use the equation of velocity to find horizontal velocity.

Complete step-by-step solution -
The solution requires thinking of the ball as a projectile (a horizontal projectile)
Look at the diagram shown below

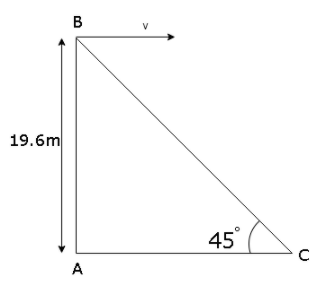
$B$ is the point from which the ball is thrown and $C$ is the point where the ball makes contact with the ground. Point $C$ makes $45^\circ $ angle with the ground.
In reality the ball would follow a parabolic path, gradually gaining vertical velocity and with a constant horizontal velocity (assuming air resistance and other interferences to be negligible) till it hits the ground. The potential and kinetic energy of the ball, will be converted into kinetic energy.
Given height$(S) = 19.6m$,\[\theta = 45^\circ \], \[u = 0\] and
We have to find out the time taken by the ball to reach the ground.
Using \[{2^{nd}}\]equation of motion, we have
\[S = ut + \dfrac{1}{2}a{t^2}\]
\[ \Rightarrow 19.6 = 0 \times t + \dfrac{1}{2} \times 9.8 \times t\](We know that\[g = 9.8m{s^{ - 1}}\])
\[ \Rightarrow 19.6 = 4.9t\]
\[ \Rightarrow t = \dfrac{{19.6}}{{4.9}}\]
\[ \Rightarrow t = 4\sec \]
Now, we have to find out the distance\[AC\].
For the\[\Delta ABC\],
\[\tan \theta = \dfrac{{AB}}{{AC}}\]
\[ \Rightarrow \tan 45^\circ = \dfrac{{19.6}}{{AC}}\]
\[ \Rightarrow 1 = \dfrac{{19.6}}{{AC}}\]
\[ \Rightarrow AC = 19.6m\]
So the ball covered \[19.6m\] horizontally in 4 sec.
Velocity\[(v)\] of a body is given by
Horizontal velocity\[ = \dfrac{{Displacement}}{{Time}}\]
\[ \Rightarrow v = \dfrac{{19.6}}{4}\]
\[ \Rightarrow v = 4.9m{s^{ - 1}}\].

Note – This problem is a classic example of projectiles, remember to always consider what the initial horizontal velocity and vertical velocity could be. Like in this problem, it is clearly stated that the ball is thrown horizontally, so there is no initial vertical velocity involved. But these conditions differ from problem to problem.