Question

From the top of a tower $ 19.6 $ m high a ball is thrown horizontally. If the line joining the point of projection to the point where it hits the ground makes an angle of $ {45^0} $ with the horizontal, then the initial velocity of the ball is:
(A) $ 9.8m{s^{ - 1}} $
(B) $ 4.9m{s^{ - 1}} $
(C) $ 14.7m{s^{ - 1}} $
(D) $ 2.8m{s^{ - 1}} $

Answer 1

Hint :Here, you must draw the suitable diagram according to the condition explained in the above question. Here the motion of the ball is projectile. You have to use the concept of projectile motion.

Complete Step By Step Answer:
We have to draw the proper diagram according to the conditions given in the question.
The diagram is as follows:

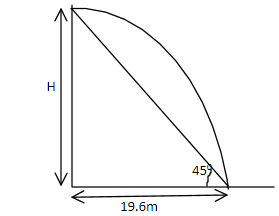
In the figure let us consider the height of tower $ H = 19.6m $
Because angle as per the figure is $ {45^0} $
Therefore, $ H = x = 19.6m $
Now, The time of flight is given by
 $ T = \sqrt {\dfrac{{2H}}{g}} $
 $ \therefore T = \sqrt {\dfrac{{2 \times 19.6}}{{9.8}}} $
 $ \therefore T = 2 $ sec
Let $ u $ be the initial velocity of the ball
Therefore, we have
 $ u = \dfrac{x}{T} $
 $ \Rightarrow $ $ u = \dfrac{{19.6}}{2} $
 $ \Rightarrow u = 9.8m{s^{ - 1}} $
Therefore, the initial velocity of the ball is obtained as $ 9.8m{s^{ - 1}} $
Correct answer is option A.

Note :
Here obtaining time of flight was important because the initial velocity of the object depends on time. The angle between the ground and the line joining the point on the ground and the tower is $ {45^0} $ then both height and the range when the ball is thrown from top of the tower is equal.