Question

From the top of a cliff 200 meters high, the angles of depression of the top and bottom of a tower are
observed to be $ 30{}^\circ $ and $ 60{}^\circ $ . Find the height of the tower and calculate the distance
between them.
A. Height = 156 m; Distance = 119.7 m
B. Height = $ 133\dfrac{1}{3} $ m; Distance = 115.46 m
C. Height = 220 m; Distance = 112.76 m
D. None of these.

Answer 1

Hint:If a person stands and looks up at an object, the angle of elevation is the angle between the horizontal line of sight and the object. If a person stands and looks down at an object, the angle of depression is the angle between the horizontal line of sight and the object.

Draw a diagram with the positions of the given structures with respect to the level ground.
Draw some right-angled triangles and identify the given angles in it.
Recall the values of trigonometric ratios for $ 30{}^\circ $ and $ 60{}^\circ $ , and use them to find the unknown lengths of the right-angled triangles.

.g. $ \sin 30{}^\circ =\dfrac{1}{2},\ \cos 30{}^\circ =\dfrac{\sqrt{3}}{2},\ \tan 30{}^\circ
=\dfrac{1}{\sqrt{3}} $
$ \sin 60{}^\circ =\dfrac{\sqrt{3}}{2},\ \cos 60{}^\circ =\dfrac{1}{2},\ \tan 60{}^\circ =\sqrt{3} $

Complete step by step solution:
Let's say that AB is the cliff and CD is the tower, as shown in the following diagram:

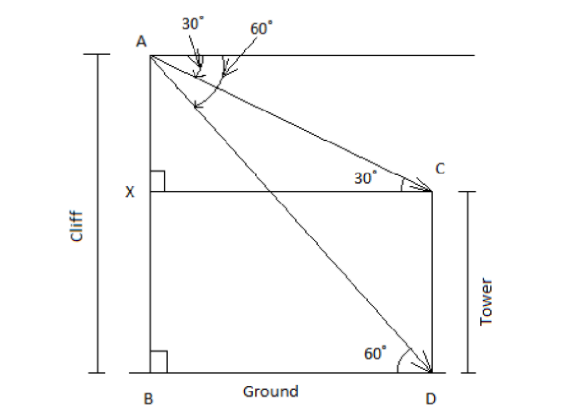
Using the definition of angle of depression and by the properties of parallel lines, we have $ \angle
ACB=30{}^\circ $ and $ \angle ADB=60{}^\circ $ . Also, $ AB=200\ m $ (height of the cliff).

Using the definition of $ \tan \theta $ in $ \Delta ABD $ , we have:
$ \tan 60{}^\circ =\dfrac{P}{B}=\dfrac{AB}{BD}=\dfrac{200}{BD} $

Using $ \tan 60{}^\circ =\sqrt{3} $ , we get:
⇒ $ \sqrt{3}=\dfrac{200}{BD} $
⇒ $ BD=\dfrac{200}{\sqrt{3}}=115.47\ m $

Now $ CX=BD=\dfrac{200}{\sqrt{3}} $ (why?). Using the definition of $ \tan \theta $ in $ \Delta AXC $ ,

we have:
$ \tan 30{}^\circ =\dfrac{P}{B}=\dfrac{AX}{XC} $

Using $ \tan 30{}^\circ =\dfrac{1}{\sqrt{3}} $ , we get:
⇒ $ AX=\dfrac{1}{\sqrt{3}}XC=\dfrac{1}{\sqrt{3}}\times
\dfrac{200}{\sqrt{3}}=\dfrac{200}{3}=66\dfrac{2}{3}\ m $
And $ CD=XB=AB-AX $ .
⇒ $ CD=200-66\dfrac{2}{3}=133\dfrac{1}{3}\ m $

The correct answer is B. Height = $ 133\dfrac{1}{3} $ m; Distance = 115.46 m.

Note:
In a right-angled triangle with length of the side opposite to angle θ as perpendicular (P), base (B) and hypotenuse (H):
$ \sin \theta =\dfrac{P}{H},\cos \theta =\dfrac{B}{H},\tan \theta =\dfrac{P}{B} $
$ {{P}^{2}}+{{B}^{2}}={{H}^{2}} $ (Pythagoras' Theorem)

If one trigonometric ratio is known, we can use Pythagoras' Theorem and calculate the values of all other trigonometric ratios.