Question

From the top of a building 20meter high, the angle of the elevation of the top of a vertical pole is ${{30}^{\circ }}$, and the angle of depression of the foot of the same pole is ${{60}^{\circ }}$. Find the height of the pole.

Answer 1

Hint: We solve this problem by assuming the height of the pole as H. Then we make a rough picture of the given information. Then we consider the tangent of angle of elevation and tangent of angle of depression using the formula, $\tan \theta =\dfrac{\text{Opposite}}{\text{Base}}$. Then we compare them to find the value of height of the pole.

Complete step-by-step answer:
We are given that angle of elevation of the top of the pole is ${{30}^{\circ }}$ and the angle of depression of the foot of the pole is ${{60}^{\circ }}$, from the top of a building of height 20m.
Let the top of the pole be P and foot of the pole be point Q and let the height of the pole be H meters.
Let the top of the building be A.

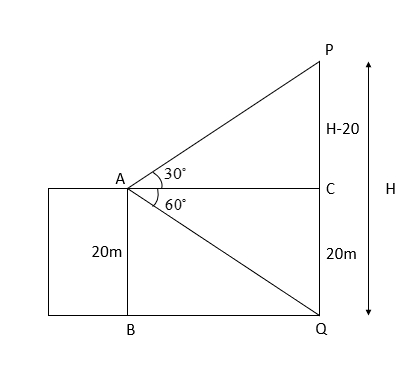
Now let us consider the triangle ACP. It is a right angled triangle with base AC. Let us consider the formula for tangent of any angle
$\tan \theta =\dfrac{\text{Opposite}}{\text{Base}}$
In $\Delta ACP$, the angle PCA is equal to ${{30}^{\circ }}$, as we are given that angle of elevation of the top of pole is ${{30}^{\circ }}$. Let us applying the tan to the angle PCA using the above formula.
$\begin{align}
  & \Rightarrow \tan \angle PAC=\dfrac{PC}{AC} \\
 & \Rightarrow \tan {{30}^{\circ }}=\dfrac{PC}{AC} \\
 & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{PC}{AC} \\
 & \Rightarrow AC=\sqrt{3}PC.............\left( 1 \right) \\
\end{align}$

Now let us consider the triangle ACQ. It is a right-angled triangle with base AC.
In $\Delta ACQ$, the angle QCA is equal to ${{60}^{\circ }}$, as we are given that angle of elevation of the top of pole is ${{60}^{\circ }}$. Let us applying the tan to the angle QCA.
$\begin{align}
  & \Rightarrow \tan \angle QAC=\dfrac{QC}{AC} \\
 & \Rightarrow \tan {{60}^{\circ }}=\dfrac{QC}{AC} \\
 & \Rightarrow \sqrt{3}=\dfrac{QC}{AC} \\
 & \Rightarrow AC=\dfrac{QC}{\sqrt{3}}.............\left( 2 \right) \\
\end{align}$
Now, as we see the equations (1) and (2), both are the values of AC. So, we can equate the equations (1) and (2).
$\begin{align}
  & \Rightarrow \sqrt{3}PC=\dfrac{QC}{\sqrt{3}} \\
 & \Rightarrow 3PC=QC \\
\end{align}$
From the diagram we can see that the lengths of PC and QC are H-20 and 20 meters respectively. So, substituting them in the above equation we get,
$\begin{align}
  & \Rightarrow 3\left( H-20 \right)=20 \\
 & \Rightarrow 3H-60=20 \\
 & \Rightarrow 3H=80 \\
 & \Rightarrow H=\dfrac{80}{3} \\
\end{align}$
So, we get that the height of the pole is $\dfrac{80}{3}$m.
Hence, the answer is $\dfrac{80}{3}$m.


Note: The main mistake one does while solving this problem is one might mistake the angle of elevation and angle of deviation. One might take the diagram as

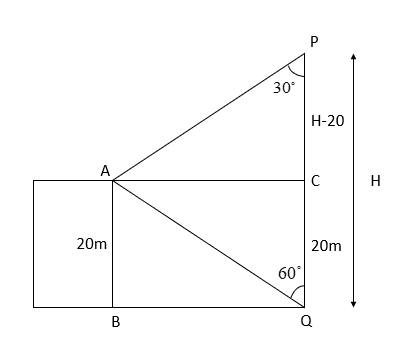
But it is wrong. The angles of elevation and depression are the angle between the line joining the object and eye and the horizontal line.