Question

From the top of a 7m height building, the angle of the elevation of a tower is $60^\circ $ and the angle of depression of the tower is $45^\circ $. Find the height of the tower.

Answer 1

Hint: To solve the above question, first we will obtain the length of distance between the building and the tower, then we will obtain the length of the tower above the height of the building. Thus by adding that value with the height of the building we will get the height of the tower.
* Angle of elevation is the upwards angle from the horizontal to a line of sight from observer to some point of interest.
* Angle of depression is the downwards angle from the horizontal to a line of sight from observer to some point of interest.
* Tangent of the angle of the right angled triangle is the ratio of perpendicular (side that is in front of that angle) to the base.

Complete step-by-step solution:
Representing the given data in the below diagram,

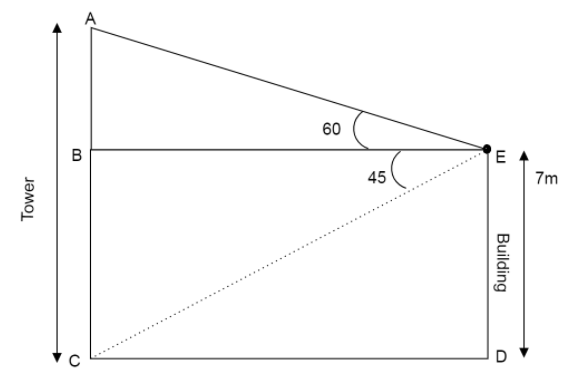
Let the height of the building be DE. Let AC be the tower having top A and bottom C.
According to the question the height of the building is 7m.
\[\therefore \] $DE = 7m.$
According to the question the angle of the elevation of top of a tower is $60^\circ $.
\[\therefore \] $\angle AEB = 60^\circ $
Again it is given that the angle of depression of the foot of the tower is $45^\circ $.
\[\therefore \]$\angle BEC = 45^\circ $
We have drawn BE parallel to CD i.e. $BE||CD$
And $BC||DE$
As Building and tower stand on the ground perpendicularly, BCDE becomes a rectangle.
\[\therefore \] $BC = DE = 7m.$
And $BE = CD$
As BCDE is on one plane, taking EC as transversal,
$\tan C = $ Perpendicular divided by base and $\angle ECD$ becomes alternative angles.
Hence, $\angle BEC = \angle ECD = 45^\circ $
In right angled triangle $\vartriangle ECD$,
ED is perpendicular and DC is base for $\angle ECD$
$\tan C = $ Perpendicular divided by base, Put the values of base and perpendicular
$ \Rightarrow \tan 45^\circ = \dfrac{{ED}}{{DC}}$
Again putting ED value and value of $\tan 45^\circ $we get,
$ \Rightarrow 1 = \dfrac{7}{{DC}}$
By cross multiplication we get,
$ \Rightarrow DC = 7$m
$\therefore $$BE = DC = 7$m
Now in right angled triangle $\vartriangle ABE$,
AB is perpendicular and BE is base for $\angle AEB$
$\therefore $$\tan \angle AEB = $ Perpendicular divided by base
Putting the values we get,
$ \Rightarrow \tan 60^\circ = \dfrac{{AB}}{{BE}}$
Again putting BE value and value of $\tan 60^\circ $we get,
$ \Rightarrow \sqrt 3 = \dfrac{{AB}}{7}$
By cross multiplication we get,
$ \Rightarrow AB = 7\sqrt 3 $m
We have taken the height of the tower as AC.
$\therefore $Height of the tower, $AC = AB + BC$
Putting values of AB and BC in the above equation we get,
$ \Rightarrow AC = 7\sqrt 3 + 7$
Taking 7 common we get,
$ \Rightarrow AC = 7(\sqrt 3 + 1)$m
$\therefore $ The height of the tower is $7(\sqrt 3 + 1)$m

Note: Many students make mistakes while cross multiplying the values from one side to another side of the equation, keep in mind we multiply the term in denominator of one side to numerator of other side and vice-versa. Also, many students make the mistake of representing the angle of depression wrong, keep in mind the angle of depression is the angle made in downward direction along with the line of sight.