Question

From the top of a 300m high lighthouse the angle of depression of the top and foot of a tower have measure $ {30^0} $ and $ {60^0} $ . Find the height of the tower.

Answer 1

Hint: Draw a proper diagram using given information. Then use the properties of $ \tan \theta $ to find relation between the different sides of the triangles. You will get two equations. Compare them to get the height of the tower.

Complete step by step solution:
Observe the diagram

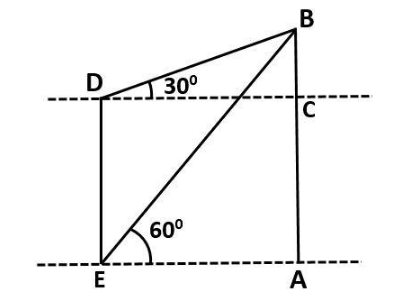
Let AB be the lighthouse and DE be the tower.
  $ \angle BEA = {60^0} $ be the angle of depression of the foot of the tower from the top of the lighthouse.
  $ \angle BDC = {30^0} $ be the angle of depression of the top of the tower from the top of the lighthouse.
  $ AB = 300m $ is the height of the lighthouse.
Now, in $ \Delta ABE $
  $ \tan {60^0} = \dfrac{{BA}}{{AE}} $
\[ \Rightarrow \sqrt 3 = \dfrac{{BA}}{{AE}}\]
Now, from the diagram, we can observe that,
  $ BA = BC + CA $
Therefore, the above equation can be written as
\[ \Rightarrow \sqrt 3 = \dfrac{{BC + CA}}{{AE}}\]
Rearranging it we can write
\[ \Rightarrow \sqrt 3 AE = BC + CA\] . . . (1)
Now, consider the $ \Delta BDC $
We can write
  $ \tan {30^0} = \dfrac{{BC}}{{DC}} $
  $ \dfrac{1}{{\sqrt 3 }} = \dfrac{{BC}}{{DC}} $
Now, from the diagram, we can observe that, $ EA = DC $
Therefore, the above equation can be written as,
  $ \dfrac{1}{{\sqrt 3 }} = \dfrac{{BC}}{{EA}} $
Rearranging it we can write
  $ EA = BC\sqrt 3 $
Now, Substitute the given values in equation (1). We get
\[3BC = BC + CA\]
Rearranging it we can write
\[2BC = CA\] . . . (2)
But we have,
  $ AB = BC + CA = 300m $
By substituting the value of BC from equation (2), in the above equation, we can write
  $ \dfrac{{CA}}{2} + CA = 300 $
By cross multiplying, we get
  $ 3CA = 600 $
  $ \Rightarrow CA = 200m $
Now, from the diagram, we can observe that,
  $ DE = CA $
  $ \Rightarrow DE = 200m $
Thus the height of the tower is $ 200m $

Note: It is important to know that the angle of depression is always equal to the angle of elevation, as they are alternate interior angles. Therefore, even though you have given an angle of depression in the question, you can use it as an angle of elevation to use it in the triangle that we form. Be sure to understand what is asked in the question, and to know, which sides will be equal to each other. Like in this equation, we could solve it because we knew that, $ DC = EA $ and $ AC = DE $ .