Question

From the second floor of a 100m tall building, the angle of depression of the bottom and top of another building exactly opposite to it are observed to be \[{{60}^{\circ }}\] and \[{{30}^{\circ }}\] respectively. What is the height of the building?
(a) 66m
(b) 67m
(c) 66.67m
(d) 65m

Answer 1

Hint: We are asked to find the length of the building opposite to the given one. We will first sketch the rough diagram then we will use the trigonometric ratio \[\tan \theta =\dfrac{\text{perpendicular}}{\text{base}},\] where perpendicular is the side in front of \[\theta \] and the base is the side below \[\theta .\] Then we will simplify the acquired value to find the required height.

Complete step by step answer:
We are given that from the second floor of 100m tall building, the angle of depression of bottom and top are \[{{60}^{\circ }}\] and \[{{30}^{\circ }}\] respectively of the opposite building. The point to understand here is from the point of observation both the angles are the angle of depression so this building whose length is to be found is smaller than the first building. So, we will draw our sketch and label as follows.

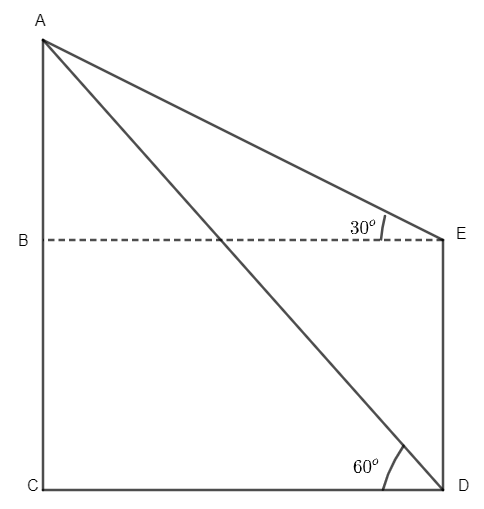
Here, AC = 100m and let the height of the other building be h m. So, ED = h m as BC = ED. So,
\[BC=hm\]
So, we can see clearly that,
\[AC=AB+BC\]
So, we get,
\[\Rightarrow 100=AB+h\]
\[\Rightarrow AB=100-h\]
Now to find the value of the height of the building, we use trigonometric ratio. In triangle ABE, we have,
\[\tan {{30}^{\circ }}=\dfrac{AB}{BE}\]
Simplifying, we get,
\[\Rightarrow BE=\dfrac{AB}{\tan {{30}^{\circ }}}\]
As, \[\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}},\] and AB = 100 – h, so we get,
\[\Rightarrow BE=\dfrac{100-h}{\dfrac{1}{\sqrt{3}}}\]
Simplifying, we get,
\[\Rightarrow BE=\sqrt{3}\left( 100-h \right)m\]
Now, in triangle ACD, we get,
\[\tan {{60}^{\circ }}=\dfrac{AC}{CD}\]
As, AC = 100 and \[\tan {{60}^{\circ }}=\sqrt{3},\] so,
\[\Rightarrow CD=\dfrac{100}{\sqrt{3}}\]
As we can see that CD = BE, so we can compare \[CD=\dfrac{100}{\sqrt{3}}\] and \[BE=\sqrt{3}\left( 100-h \right).\] So,
\[\left( 100-h \right)\sqrt{3}=\dfrac{100}{\sqrt{3}}\]
On simplifying, we get,
\[\Rightarrow \left( 100-h \right)3=100\]
\[\Rightarrow 300-3h=100\]
Solving for h, we get,
\[\Rightarrow h=\dfrac{200}{3}\]
So,
\[\Rightarrow h=66.67m\]
So, the height of the building is 66.67m.
Therefore, option (c) is the right answer.

Note:
Always remember that as we increase the angle, the value of tan keeps on increasing so students shouldn’t be confused. With the value of \[\tan {{30}^{\circ }}\] as \[\sqrt{3}\] the value of \[\tan {{30}^{\circ }}\] is \[\dfrac{1}{\sqrt{3}}\] while the value of \[\tan {{60}^{\circ }}\] is \[\sqrt{3}.\] Also keep track that the angle of depression will keep on increasing as more downward you keep on looking.

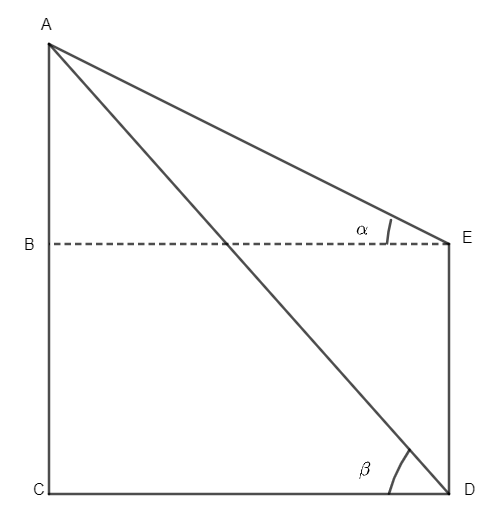
So, \[\beta >\alpha \] always.