Question

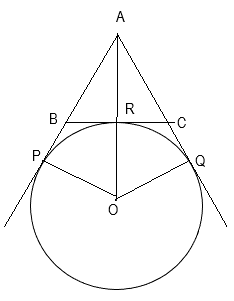
From the given figure, find the perimeter of \[\Delta ABC\], if \[AP = 10cm\].

Answer 1

Hint: We will use the properties of tangents of a circle to find the perimeter of the required triangle. The main property to be used is that the tangents drawn to a circle from an exterior point are equal.

Complete step by step Answer :

We are given that \[AP = 10cm\].
We know that the tangents drawn to a circle from an exterior point are equal. Hence, \[AQ = AP = 10cm\]
In the \[\Delta OPB\& \Delta OBR,\]
\[
  OR = OP[\because radius] \\
  OB\; is \;common \\
  \angle OPB = \angle ORB = {90^ \circ } \\
\]
(\[\angle OPB = \angle ORB = {90^ \circ }\] because at the point of intersection, angle between the radius and the tangent is \[{90^ \circ }\])
Hence, \[\Delta OPB\& \Delta OBR\]are congruent with the R.H.S. property.
\[PB = BR\][corresponding parts of two congruent triangles are equal]
In the \[\Delta OCQ\& \Delta OCR,\]
\[
  OR = OQ[\because radius] \\
  OC\; is \;common \\
  \angle ORC = \angle OQC = {90^ \circ } \\
\]
(\[\angle OQC = \angle ORC = {90^ \circ }\] because at the point of intersection, angle between the radius and the tangent is\[{90^ \circ }\])
Hence, \[\Delta OCQ\& \Delta OCR\]are congruent with the R.H.S. property.
We will then get \[CR = CQ\]as corresponding parts of two congruent triangles are equal.
The Perimeter of the\[\Delta ABC\]
\[
   = AB + BC + AC \\
   = (AP - BP) + (BR + RC) + (AQ - CQ) \\
   = AP - BP + BR + RC + AQ - CQ \\
   = AP - BR + BR + RC + AQ - RC \\
   = AP + AQ \\
   = 10 + 10 \\
   = 20cm \\
\]

Therefore, the perimeter of\[\Delta ABC = 20cm\].

Note: In these types of questions where the two tangents are given, we will have to use the property that the tangents drawn to a circle from an exterior point are equal. We also need to keep in mind that tangents and radii are perpendicular to each other at the point of intersection. It is necessary for us to prove the congruence of the triangles in order to find the lengths of the tangent \[BC\].