Question

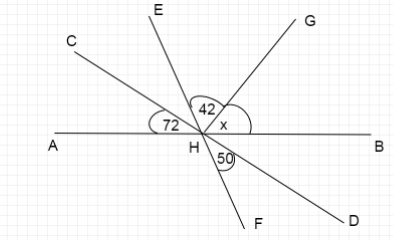
From the given figure, \[AHB,CHD,EHF\]are three straight lines. Find the value of \[x\]

Answer 1

Hint:Here using the information of three lines intersecting each other, we compare the vertically opposite angles formed by the lines \[CHD\] and \[EFH\] and then using the concept of sum of all angles on a straight line sums up to \[{180^ \circ }\] we find the value of \[x\]

Complete step-by-step answer:
We first take the pair of straight lines \[CHD\] and \[EFH\] that intersect at point \[H\]
Since, we know vertically opposite angles are \[\angle CHE,\angle FHD\]
Therefore from the property of vertically opposite angles we can write
\[\angle CHE = \angle FHD\]
Since we are given the value of \[\angle FHD = {50^ \circ }\]
Therefore, \[\angle CHE = {50^ \circ }\]
Now we look at the straight line \[AHB\] and use the property that sum of all angles on a straight line equals to \[{180^ \circ }\].
Therefore angles on the line \[AHB\] are \[\angle AHC,\angle CHE,\angle EHG,\angle GHB\]
Adding all the angles
\[\angle AHC + \angle CHE + \angle EHG + \angle GHB = {180^ \circ }\]
Substituting the values of \[\angle AHC = {72^ \circ },\angle CHE = {50^ \circ },\angle EHG = {42^ \circ },\angle GHB = x\]
\[
  {72^ \circ } + {50^ \circ } + {42^ \circ } + x = {180^ \circ } \\
  {164^ \circ } + x = {180^ \circ } \\
 \]
Taking the values of degree given on the RHS of the equation
\[x = {(180 - 164)^ \circ } = {16^ \circ }\]
Therefore, value of \[x = {16^ \circ }\]

Note:Students are advised to draw the diagram for better understanding.
Alternative method:
Here we take take the pair of straight lines \[CHD\] and \[EFH\] that intersect at point \[H\]
Since, we know vertically opposite angles are \[\angle CHE,\angle FHD\]
Therefore from the property of vertically opposite angles we can write
\[\angle CHE = \angle FHD\]
Since we are given the value of \[\angle FHD = {50^ \circ }\]
Therefore, \[\angle CHE = {50^ \circ }\]
Similarly from pair of straight lines \[CHD\] and \[AHB\] that intersect at point \[H\]
Since, we know vertically opposite angles are \[\angle AHC,\angle BHD\]
Therefore from the property of vertically opposite angles we can write
\[\angle AHC = \angle BHD\]
Since we are given the value of \[\angle AHC = {72^ \circ }\]
Therefore, \[\angle BHD = {72^ \circ }\]
Now we look at the straight line \[EHF\] and use the property that the sum of all angles on a straight line equals \[{180^ \circ }\].
Therefore angles on the line \[EHF\] are \[\angle FHD,\angle BHD,\angle EHG,\angle GHB\]
Adding all the angles
\[\angle FHD + \angle BHD + \angle EHG + \angle GHB = {180^ \circ }\]
Substituting the values of \[\angle DHB = {72^ \circ },\angle FHD = {50^ \circ },\angle EHG = {42^ \circ },\angle GHB = x\]
\[
  {72^ \circ } + {50^ \circ } + {42^ \circ } + x = {180^ \circ } \\
  {164^ \circ } + x = {180^ \circ } \\
 \]
Taking the values of degree given on the RHS of the equation
\[x = {(180 - 164)^ \circ } = {16^ \circ }\]
Therefore, value of \[x = {16^ \circ }\]