Question

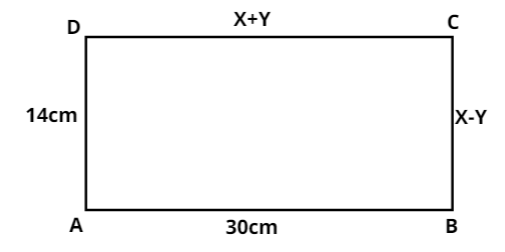
From the below figure, $ABCD$ is a rectangle. Find the values of $x$ and $y$.

Answer 1

Hint: The opposite sides of a rectangle are always equal in length. So, for a rectangle $ABCD$,
$AB = CD$ and $BC = AD$.

Complete step-by-step answer:
Given, $ABCD$ is a rectangle in which
$AB = 30cm$, $BC = \left( {x - y} \right)$, $CD = \left( {x + y} \right)$ and $AD = 14cm$
Since $ABCD$ is a rectangle and we know that the opposite sides of a rectangle are equal.
Hence, $AB = CD$
$ \Rightarrow 30 = x + y$
$ \Rightarrow x + y = 30$ …. (1)
Also, $BC = AD$
$ \Rightarrow x - y = 14$ …. (2)
Adding equation (1) and (2), we get
$\left( {x + y} \right) + \left( {x - y} \right) = 30 + 14$
$ \Rightarrow 2x = 44$
$ \Rightarrow x = \dfrac{{44}}{2}$
$ \Rightarrow x = 22$
Putting $x = 22$ in equation (1)
$22 + y = 30$
$ \Rightarrow y = 30 - 22$
$ \Rightarrow y = 8$

The value of X is 22 and Y is 8.

Note: Rectangle is a type of quadrilateral with 4 sides and 4 interior angles which are equal to $90^\circ$. The sum of all the angles in a triangle is equal to $360^\circ$. There are 2 diagonals which intersect at the center of the rectangle.