Question

How far from the base of the house do you need to place a $15$- foot ladder so that it exactly reaches the top of a $12$- foot tall wall?

Answer 1

Hint: In this question, we have been asked to find the distance between the foot of a ladder and the wall. This question is of the topic – Pythagoras theorem. Draw a figure of the given question. And put the values in the theorem and simplify to find the answer.

Complete step-by-step solution:
We are given the height of the ladder and the wall and we have been asked to find the distance between them. We will assume that the ladder is tilted towards the wall. Let us draw this figure.

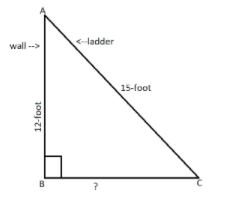
As we can see in the figure, the wall is denoted by $AB$, the ladder is denoted by $AC$, and we have to find the distance between the wall and the foot of the ladder. This distance is denoted by $BC$. Since the triangle formed is a right-angled triangle, we can use Pythagoras theorem to find the answer.
We know that, ${H^2} = {P^2} + {B^2}$.
$ \Rightarrow A{C^2} = A{B^2} + B{C^2}$
Putting all the values,
$ \Rightarrow {15^2} = {12^2} + B{C^2}$
Simplifying the equation,
$ \Rightarrow 225 = 144 + B{C^2}$
Shifting to find the values,
$ \Rightarrow 225 - 144 = B{C^2}$
Let us subtract the term and we get
$ \Rightarrow 81 = B{C^2}$
Square rooting both the sides,
$ \Rightarrow BC = \pm 9$

Since the distance cannot be negative, our answer will be $9$-foot.

Note: Pythagoras theorem: This theorem says that “In a right-angled triangle, the square of hypotenuse is equal to the sum of the squares of the base and the perpendicular.” In such a triangle, hypotenuse is the longest side.
A very common Pythagorean triplet is $3,4,5$. A point to be noted is that the multiples of this Pythagorean triplet are also Pythagorean triplets. For example: In this question, the triplet that came up was $9,12,15$. This triplet is also a multiple of $3,4,5$.