Question

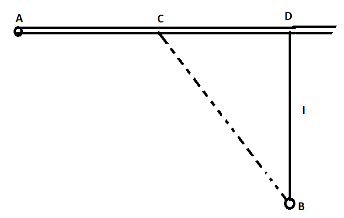
From point A located on the highway (shown in the figure below) one has to get by car as soon as possible to point B located in the field at a distance $l$ from the highway. It is known that the car moves in the field $\eta $ times slower than on the highway. At a distance CD$ = \dfrac{{xl}}{{\sqrt {{\eta ^2} - 1} }}$ from point D one must turn off the highway. Find x.

Answer 1

Hint:In this question, we are given that the car is moving on a highway with given velocity. Then we have to find the value x along the path CD. To find x, we are letting this distance CD=x for our convenience. Find the total period and then apply the condition for maxima. And hence we got our answer.

Complete step by step answer:
Let the car turn off the highway at a distance $x$ from the point D. Taking $CD = x$ and the speed of the car in the field be $v$, then time taken by the car to cover distance AC be taken as ${t_1}$.

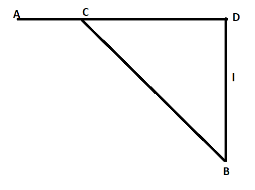
Calculating, from the diagram $AC = AD - x$ and we are given that on the highway speed of the car is $\eta $ times slower. Hence take velocity to be $\eta v$
${t_1} = \dfrac{{AD - x}}{{\eta v}}$ $ \ldots \left( 1 \right)$
Now, the car moves to the distance CB. Finding the time taken by car to cover distance CB. From the diagram, $CB = \sqrt {{l^2} + {x^2}} $
${t_2} = \dfrac{{\sqrt {{l^2} + {x^2}} }}{v}$ $ \ldots \left( 2 \right)$
Now, finding total time taken by car to cover the distance AB.
$T = {t_1} + {t_2}$
$\Rightarrow T = \dfrac{{AD - x}}{{\eta v}} + \dfrac{{\sqrt {{l^2} + {x^2}} }}{v}$ $ \ldots \left( 3 \right)$
According to the question, one has to get up the car as soon as possible. This statement states that we have to reach point B as soon as possible. Hence, applying the condition of maxima
So, differentiating $\left( 3 \right)$ with respect to x and equating to zero.
$\dfrac{{dT}}{{dx}} = 0$
$\Rightarrow \dfrac{1}{v}\left[ { - \dfrac{1}{\eta } + \dfrac{x}{{\sqrt {{l^2} + {x^2}} }}} \right] = 0$
$
\Rightarrow{\eta ^2}{x^2} = {l^2} + {x^2} \\
\therefore x = \dfrac{1}{{\sqrt {{\eta ^2} - 1} }} \\ $
Hence, the value of x is $\dfrac{1}{{\sqrt {{\eta ^2} - 1} }}$.

Note:Choose the variables along the distance wisely. We must know about the condition for maxima which is differentiating with a variable and equating to zero.The terms velocity and speed give us an idea of how fast or slow an object is moving. Quite often, we come across situations where we need to identify which of the two or more objects is moving faster. One can easily tell the fastest of the two if they are moving in the same direction on the same road.