Question

From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in figure. Find the area of the remaining portion of the square.

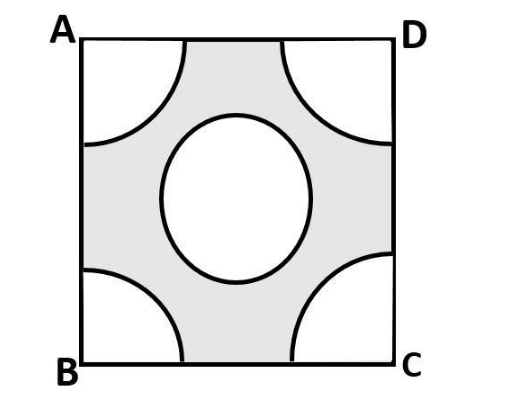
Answer 1

Hint:Find the area of the square. Then find the area of all the portions that are cut from the square. Then subtract the area of the portion that is cut from the area of the square. The answer will be the remaining area.

Complete step-by-step answer:

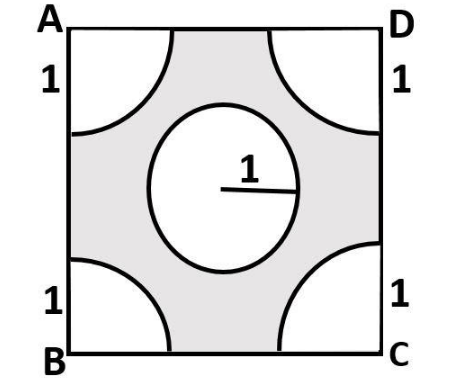
It is given in the question that ABCD is a square with side, say, $ a = 4cm $
A quadrant of radius, say, $ r = 1cm $ is cut from all four corners of the square.
Now, we can observe that a quadrant is the fourth part of a circle. That means, four quadrants will form one circle. Thus the area cut by four quadrants will be equal to the area cut by one circle.
Also, a circle of diameter 2 cm is cut from the center. But diameter is two times the radius. That means, a circle of radius 1 cm is cut from the center.
But the quadrants also have radius one. Means the radius of the circle that is cut from the center and the radius of the circle that is formed by adding the four quadrants is equal.
Thus, their area will also be equal.
Therefore, we can conclude that the area in the shaded region will be equal to the difference of area of a square whose side is 4 cm and two times the area of a circle whose radius is 1 cm
It can mathematically be written as,
 $\Rightarrow A = {a^2} - 2\pi {r^2} $
By substituting the given values in the above equation, we get
 $ A = {4^2} - 2\pi \times 1 $
 $ \Rightarrow A = 16 - 2\pi $
Therefore, the area of the shaded region is $ 16 - 2\pi $
So, the correct answer is “Option A”.

Note: Understanding that the four quadrants will make one circle and the area of the circle formed by the quadrants and the circle that was cut from the center is the same made the question easy and short. You can always remember the logic that the area of the shaded region is the difference between the total area and the area of the unshaded region.