Question

From a window 15 m high above the ground in a street, the angles of elevation and depression of the top and foot off another house on the opposite side of the street are 30 and 45 degrees, respectively. Show that the height of the opposite house is 23.66 m. [take $\sqrt{3}=1.732$].

Answer 1

Hint: Let the window be at P at a height of 15m above the ground. Let CD be the house on the opposite side of the street having height as h meter. Let AP is the length of the window above the ground street which is 15 m high. Using tan 45 degree in triangle PQC, we find the value of PQ. After applying tan 30 degree angle in triangle PQD, we find the value of DQ. At the end by adding both DQ and QC we get the value h.

Complete step-by-step answer:
Let the window be at P at a height 15 m above the ground.

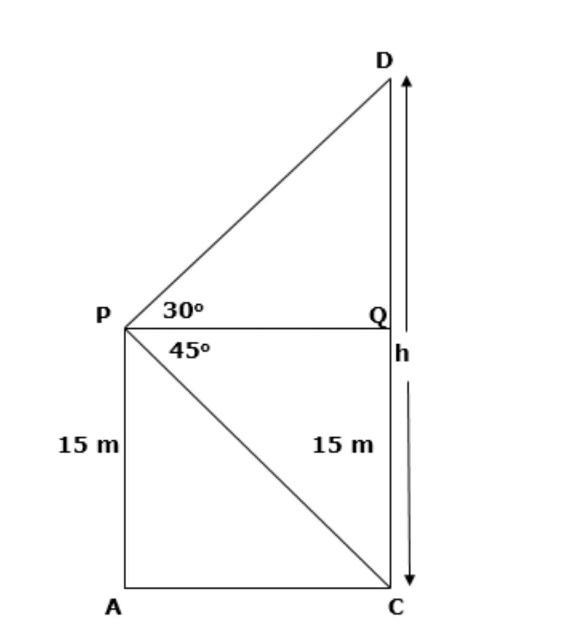
Let the height of the house CD $=\text{ h meters}$.

Now,
QD = CD – CQ =CD – AP =$\left( h-15 \right)metres$.
Consider triangle PQC, applying $\tan {{45}^{\circ }}$ in it to get the value of PQ.

In triangle PQC,
$\tan {{45}^{\circ }}=\dfrac{QC}{PQ}$

The value of $\tan {{45}^{\circ }}=1$ and the value of QC is 15m.
$\begin{align}
  & \Rightarrow 1=\dfrac{15}{PQ} \\
 & \Rightarrow PQ=15meters \\
\end{align}$

Now, consider triangle PQC, applying $\tan {{30}^{0}}$ in it to get the value of h.

In triangle PQD,
$\tan {{30}^{\circ }}=\dfrac{QD}{PQ}$
The value of $\tan {{30}^{\circ }}$ is $\dfrac{1}{\sqrt{3}}$.

Let the value of QD be $\left( h-15 \right)$ and the value of PQ is $15$m.
$\begin{align}
  & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{h-15}{15} \\
 & \Rightarrow h-15=\dfrac{15}{\sqrt{3}} \\
 & \Rightarrow h=15+\dfrac{15}{\sqrt{3}} \\
 & \Rightarrow h=15+15\sqrt{3} \\
 & \Rightarrow h=5\left( 3+\sqrt{3} \right)=5(3+1.732)=5\times 4.732 \\
 & \Rightarrow h=23.66m \\
\end{align}$

The height of the opposite house is $23.66m$ as you see above.
Hence, the height of the opposite house is $23.66m$.

Note: The key step for solving this problem is the knowledge of trigonometry in geometrical mathematics. By using trigonometry, we can calculate the value of height of a complex system in seconds by measuring the angle of elevation from a fixed surface.