Question

From a top of a cliff 25 m high, the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
A. 25 m
B. 50 m
C. 75 m
D. 100 m

Answer 1

Hint: The angle of elevation is the angle above the eye level of the observer towards a given point. The angle of depression is the angle below the eye level of the observer towards a given point. The tangent function is the ratio of the opposite side and the adjacent side.

Complete step-by-step answer:

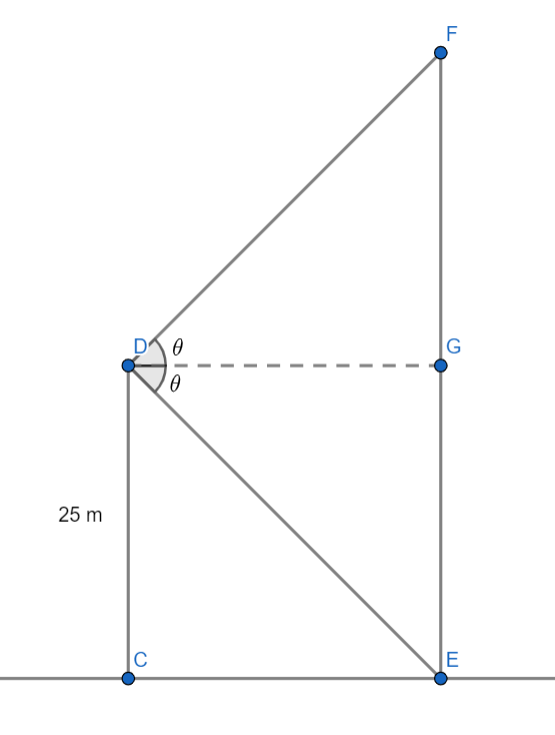
This is the diagram of the given question. CD is the cliff of height 25 m and EF is the tower with base E and top F. Let $\theta $ be the angle of elevation and depression. From the given figure we can see that-

CD = EG = 25 m ….(1)

Applying trigonometric ratios in triangles DGE and DGF,

$\begin{gathered}

  tan\theta = \dfrac{{EG}}{{DG}} \\

  tan\theta = \dfrac{{FG}}{{DG}} \\

\end{gathered} $

By comparing the two values we can see that,

$\dfrac{{EG}}{{DG}} = \dfrac{{FG}}{{DG}}$

EG = FG

Using equation (1), we can see that

EG = FG = 25 m

The height of the tower is

EF = EG + GF

EF = 25 + 25

EF = 50 m

This is the required answer.


Note: In such types of questions, it is important to read the language of the question carefully and draw the diagram step by step correctly. When the diagram is drawn, we just have to apply basic trigonometry to find the required answer.