Question

From a square cardboard, a circle of the biggest area was cut out. If the area of the circle is $154c{m^2}$ , calculate the original area of the cardboard.

Answer 1

Hint: Here, because the circle is of the biggest area that is cut out from the cardboard. Therefore, we can take the diameter of the circle equal to the side of the square cardboard. Then, from the area of the circle, we can evaluate the radius.

Formula used: Area of Circle: $\pi {r^2}$ , where $r$ is the radius of the circle
Area of Square: $side \times side$

Complete step-by-step solution:
Here, as we know that from a square cardboard, a circle of the biggest area is cut out.

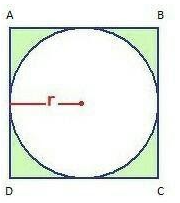
From the figure, let us assume that $\;ABCD$ represents the square cardboard and $r$ represents the radius of the circle that was cut out from $\;ABCD$ .
It is given that the area of the circle is $154c{m^2}$ ,
So by using the formula of the area of the circle, we can find the radius.
We know that,
Area of circle = $\pi {r^2}$
Here, we substitute the given area of the circle and take $\pi = \dfrac{{22}}{7}$ ,
$\Rightarrow 154 = \dfrac{{22}}{7} \times {r^2}$
$\Rightarrow {r^2} = \dfrac{{154 \times 7}}{{22}}$
Now, after simplifying, we get
$\Rightarrow {r^2} = 7 \times 7$
$\Rightarrow {r^2} = 49$
Now, after evaluating the square root, we get
$\Rightarrow r = \pm 7$
Now, we know that radius of a circle cannot be negative, so we take
$\Rightarrow r = 7cm$
Now, we get the radius of the circle is $\;7cm$, so
Diameter of circle =$2 \times radius$
$\Rightarrow d = 2 \times 7$ , where $d$ is the diameter
$\Rightarrow d = 14$
∴ Diameter is $\;14cm$ , then we take the side of the square $\;ABCD$ , equal to .
Now, we need to find out the area of a square $\;ABCD$ ,
And, we know that, area of square $\;ABCD$=$side \times side$
$= 14 \times 14$
$= 196c{m^2}$

The original area of the cardboard is $196c{m^2}$ .

Note: Here, the diameter of the circle is equal to the side of the square cardboard. This can be easily verified from the figure in the solution part. Thus, we take the diameter of the circle equal to the side of the square, and using this we completed the solution part.