Question

From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the Circle is 12 cm. Find the radius of the circle.

Answer 1

Hint: A point Q is 13 cm away from the centre of the circle and PQ is a tangent to the circle which means P is a point on the circle. A tangential point makes a right angle with the centre of the circle. Use Pythagoras theorem to solve for the radius of the circle.

Complete step-by-step answer:

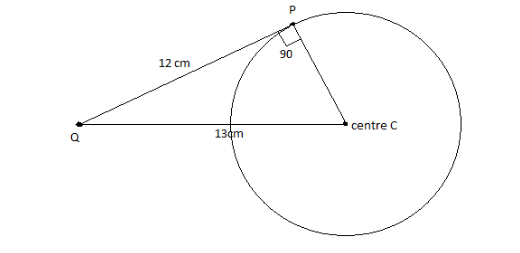
We are given that a point Q is 13 cm away from the centre C of a circle. PQ is a tangent to the circle so a line is drawn from Q to P where P is a point on the circle.
We have to find the radius of the circle.
As we can see in the above diagram, a tangent makes a right angle with the radius of the circle.
 So PQC is a right angled triangle. By Pythagoras theorem, hypotenuse square is equal to the sum of the squares of its adjacent sides.
Hypotenuse= QC= 13 cm
Tangent= Adjacent side= PQ= 12 cm
Radius=?
 $
  Q{C^2} = P{Q^2} + P{C^2} \\
  QC = 13cm,PQ = 12cm \\
  {13^2} = {12^2} + P{C^2} \\
  P{C^2} = {13^2} - {12^2} \\
  P{C^2} = 169 - 144 \\
  P{C^2} = 25 \\
  PC = \sqrt {25} = 5cm \\
 $
Therefore, the value of the PC which is the radius of the circle is 5 cm.

Note: Tangents drawn from a single point outside of the circle to the circle are always congruent. Tangent intersects the circle only at one point whereas a secant intersects a circle at two points. So do not confuse a tangent with a secant.