Question

From a point on the horizontal plane, the elevation of the top of a hill is \[{{45}^{\circ }}.\] After walking 500m in towards its summit up a slope inclined at an angle of \[{{15}^{\circ }}\] to the horizon, the elevation is \[{{75}^{\circ }},\] the height of the hill is:
\[\left( a \right)500\sqrt{6}m\]
\[\left( b \right)500\sqrt{3}m\]
\[\left( c \right)250\sqrt{6}m\]
\[\left( d \right)250\sqrt{3}m\]

Answer 1

Hint: First of all draw a figure according to the information given in the question. Then we will use the suitable trigonometric ratios like \[\sin {{30}^{\circ }},\cos {{30}^{\circ }},\sin {{45}^{\circ }},\cos {{45}^{\circ }},etc.\] to get the required value.

Complete step by step answer:
In this question, we are given that from a point on the horizontal plane, the elevation of the top of a hill is \[{{45}^{\circ }}.\] After walking 500m in towards its summit up a slope inclined at an angle of \[{{15}^{\circ }}\] to the horizon, the elevation is \[{{75}^{\circ }}.\] And we have to find the value of the height of the hill.
Let us first draw a figure according to the given information.

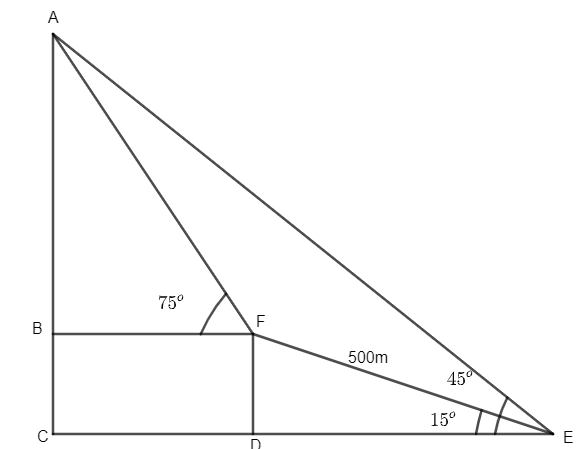
In the above figure, we have assumed that
AC is the height of the hill
\[\angle AEC={{45}^{\circ }}=\text{ the angle of elevation of the top of the hill}\]
\[\angle FED={{15}^{\circ }}=\text{ the angle of inclination of the slope to the horizontal}\]
EF = 500m = distance of the slope
\[\angle AFB={{75}^{\circ }}=\text{ the angle of elevation after walking 500m up the slope}\]
Let us consider triangle FDE from the figure. We know that \[\sin \theta =\dfrac{\text{perpendicular}}{\text{hypotenuse}}.\] By using these, we get,
\[\sin {{15}^{\circ }}=\dfrac{FD}{EF}.....\left( i \right)\]
We can write \[\sin {{15}^{\circ }}=\sin \left( {{45}^{\circ }}-{{30}^{\circ }} \right).\]
We know that sin (A – B) = sin A cos B – cos A sin B. By using this, we get,
\[\Rightarrow \sin {{15}^{\circ }}=\sin {{45}^{\circ }}\cos {{30}^{\circ }}-\cos {{45}^{\circ }}\sin {{30}^{\circ }}\]
From the table of trigonometric ratios of standard angles, we know that,
\[\sin {{45}^{\circ }}=\cos {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}\]
\[\cos {{30}^{\circ }}=\dfrac{\sqrt{3}}{2}\]
\[\sin {{30}^{\circ }}=\dfrac{1}{2}\]
By using this, we get,
\[\Rightarrow \sin {{15}^{\circ }}=\dfrac{1}{\sqrt{2}}.\dfrac{\sqrt{3}}{2}-\dfrac{1}{\sqrt{2}}.\dfrac{1}{2}\]
\[\Rightarrow \sin {{15}^{\circ }}=\dfrac{\sqrt{3}-1}{2\sqrt{2}}\]
By substituting the value of \[\sin {{15}^{\circ }}\] in equation (i), we get,
\[\Rightarrow \dfrac{\sqrt{3}-1}{2\sqrt{2}}=\dfrac{FD}{EF}\]
From the figure, we know that EF = 500m. So, we get,
\[\Rightarrow \dfrac{\sqrt{3}-1}{2\sqrt{2}}=\dfrac{FD}{500}\]
\[\Rightarrow FD=\dfrac{\sqrt{3}-1}{2\sqrt{2}}\times 500\]
\[\Rightarrow FD=250\left( \dfrac{\sqrt{3}-1}{\sqrt{2}} \right)m......\left( ii \right)\]
We also know that \[\cos \theta =\dfrac{\text{base}}{\text{hypotenuse}}.\]
So, in triangle FDE, we get, \[\cos {{15}^{\circ }}=\dfrac{ED}{EF}.\]
In the similar way, we get \[\cos {{15}^{\circ }}=\dfrac{\sqrt{3}+1}{2\sqrt{2}}.\] So, we get,
\[\Rightarrow \dfrac{ED}{EF}=\dfrac{\sqrt{3}+1}{2\sqrt{2}}\]
We know that EF = 500m. So, we get,
\[\Rightarrow \dfrac{\sqrt{3}+1}{2\sqrt{2}}=\dfrac{ED}{500}\]
So, we get,
\[\Rightarrow ED=\left( 500 \right)\left[ \dfrac{\sqrt{3}+1}{2\sqrt{2}} \right]\]
\[\Rightarrow ED=\left( 250 \right)\left( \dfrac{\sqrt{3}+1}{\sqrt{2}} \right)m......\left( iii \right)\]
Now let us consider triangle ACE, we know that \[\tan \theta =\dfrac{\text{perpendicular }}{\text{base}}.\]
So, we get \[\tan {{45}^{\circ }}=\dfrac{AC}{EC}.\] We know that \[\tan {{45}^{\circ }}=1.\] So, we get,
\[1=\dfrac{AC}{EC}\]
\[AC=EC......\left( iv \right)\]
Now, let us consider triangle ABF, we get,
\[\tan {{75}^{\circ }}=\dfrac{AB}{BF}.....\left( v \right)\]
We can write \[\tan {{75}^{\circ }}=\tan \left( {{45}^{\circ }}+{{30}^{\circ }} \right).\]
We also know that, \[\tan \left( A+B \right)=\dfrac{\tan A+\tan B}{1-\tan A\tan B}.\]
By using this formula, we get,
\[\tan {{75}^{\circ }}=\dfrac{\tan {{45}^{\circ }}+\tan {{30}^{\circ }}}{1-\tan {{45}^{\circ }}\tan {{30}^{\circ }}}\]
We know that \[\tan {{45}^{\circ }}=1\] and \[\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}.\] So, we get,
\[\Rightarrow \tan {{75}^{\circ }}=\dfrac{1+\dfrac{1}{\sqrt{3}}}{1-\dfrac{1}{\sqrt{3}}}\]
\[\Rightarrow \tan {{75}^{\circ }}=\dfrac{\left( \sqrt{3}+1 \right)}{\left( \sqrt{3}-1 \right)}\times \dfrac{\left( \sqrt{3}+1 \right)}{\left( \sqrt{3}+1 \right)}\]
\[\Rightarrow \tan {{75}^{\circ }}=2+\sqrt{3}\]
By substituting the value of \[\tan {{75}^{\circ }}\] in equation (v), we get,
\[\Rightarrow \left( 2+\sqrt{3} \right)=\dfrac{AB}{BF}\]
From the figure, we can also write the above equation as
\[\Rightarrow \left( 2+\sqrt{3} \right)=\dfrac{AC-BC}{BF}\]
From the figure, we can see that BF = CD and FD = BC. So, we get,
\[\Rightarrow \left( 2+\sqrt{3} \right)=\dfrac{AC-BC}{CD}\]
\[\Rightarrow \left( 2+\sqrt{3} \right)=\dfrac{AC-BC}{EC-ED}\]
By substituting the values of BC, ED and EC from equation (ii), (iii) and (iv) respectively, we get,
\[\Rightarrow \left( 2+\sqrt{3} \right)=\dfrac{AC-250\left( \dfrac{\sqrt{3}-1}{\sqrt{2}} \right)}{AC-250\left( \dfrac{\sqrt{3}+1}{\sqrt{2}} \right)}\]
\[\Rightarrow \left( 2+\sqrt{3} \right)=\dfrac{\sqrt{2}AC-250\left( \sqrt{3}-1 \right)}{\sqrt{2}AC-250\left( \sqrt{3}+1 \right)}\]
By cross multiplying the above equation, we get,
\[\Rightarrow \left( 2+\sqrt{3} \right)\left( \sqrt{2}AC-250\left( \sqrt{3}+1 \right) \right)=\left[ \sqrt{2}AC-250\left( \sqrt{3}-1 \right) \right]\]
\[\Rightarrow 2\sqrt{2}AC-500\left( \sqrt{3}+1 \right)+\sqrt{6}AC-250\sqrt{3}\left( \sqrt{3}+1 \right)=\sqrt{2}AC-250\left( \sqrt{3}-1 \right)\]
By taking all the constant terms to the RHS, we get,
\[\Rightarrow 2\sqrt{2}AC+\sqrt{6}AC-\sqrt{2}AC=500\left( \sqrt{3}+1 \right)+250\sqrt{3}\left( \sqrt{3}+1 \right)-250\left( \sqrt{3}-1 \right)\]
\[\Rightarrow AC\left( 2\sqrt{2}+\sqrt{6}-\sqrt{2} \right)=500\sqrt{3}+500+750+250\sqrt{3}-250\sqrt{3}+250\]
By cancelling the opposite terms, we get,
\[\Rightarrow AC\left( \sqrt{2}+\sqrt{6} \right)=500\sqrt{3}+1500\]
\[\Rightarrow AC\sqrt{2}\left( 1+\sqrt{3} \right)=500\sqrt{3}\left( 1+\sqrt{3} \right)\]
\[\Rightarrow AC=\dfrac{500\sqrt{3}\left( 1+\sqrt{3} \right)}{\sqrt{2}\left( 1+\sqrt{3} \right)}\]
By cancelling the like terms and multiplying \[\sqrt{2}\] on both the numerator and denominator, we get,
\[\Rightarrow AC=\dfrac{500\sqrt{6}}{2}\]
\[\Rightarrow AC=250\sqrt{6}m\]

So, the correct answer is “Option c”.

Note: In these types of questions, it is very important to draw the figure to clearly visualize the question and use it in the solution wherever necessary. Also, students must remember the trigonometric ratios of the standard angles like \[{{0}^{\circ }},{{30}^{\circ }},{{45}^{\circ }},{{60}^{\circ }},{{90}^{\circ }},etc.\] to easily solve these type of questions as we can find other angles using these angles. Also, take care of the calculations while solving the question and properly use the trigonometric ratios as well.