Question

From a point on a bridge across a river the angles of depression of the banks on opposite sides of the river are \[{{30}^{\circ }}\] and \[{{45}^{\circ }}\] respectively. If the bridge is at a height of 4m from the banks, find the width of the river.

Answer 1

Hint: In this question, first draw the diagram it will give us a clear picture of what we have to find out. From the diagram consider the triangles formed then by using the tangent formula get the value of the sides. Then the width of the river can be found from those sides.
\[\tan \theta =\dfrac{opposite}{adjacent}\]

Complete step-by-step answer:

Let us first draw the diagram from the given conditions and analyse.

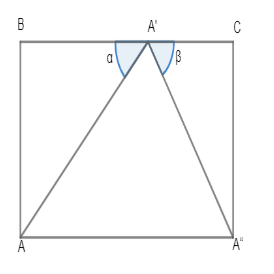
Let us assume that A" and A are two sides of the banks and A' is a point on the bridge.
Given, AB = A"C = 4m
\[\begin{align}
  & \alpha ={{30}^{\circ }} \\
 & \beta ={{45}^{\circ }} \\
\end{align}\]
As we already know that,
\[\tan \theta =\dfrac{opposite}{adjacent}\]
Let us first consider the triangle ABA':
Here, on applying the above tangent formula we get,
\[\tan \alpha =\dfrac{AB}{BA'}\]
Assume BA' as some x.
Now, by substituting this we get,
By substituting the values AB = 4, BA' = x,
\[\Rightarrow \tan \alpha =\dfrac{4}{x}\]
As we already know that \[\alpha ={{30}^{\circ }}\]. So, by substituting this we get,
\[\Rightarrow \tan {{30}^{\circ }}=\dfrac{4}{x}\]
Here, by substituting the respective values in the above equation we get,
\[\begin{align}
  & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{4}{x}\text{ }\left[ \because \tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}} \right] \\
 & \therefore x=4\sqrt{3}m \\
\end{align}\]
Now, on considering the triangle A"CA' we get,
By applying the above tangent formula to this triangle we get,
\[\tan \beta =\dfrac{A''C}{CA'}\]
Now, assume CA' as y.
Here, by substituting the values A"C = 4 and CA' = y we get,
\[\Rightarrow \tan \beta =\dfrac{4}{y}\]
As we already know that \[\beta ={{45}^{\circ }}\]. So, by substituting that in the above equation we get,
\[\Rightarrow \tan {{45}^{\circ }}=\dfrac{4}{y}\]
Here, by substituting the respective values in the equation we get,
\[\begin{align}
  & \Rightarrow 1=\dfrac{4}{y}\text{ }\left[ \because \tan {{45}^{\circ }}=1 \right] \\
 & \therefore y=4m \\
\end{align}\]
Now, the width of the river is nothing but the distance BC.
\[\begin{align}
  & \Rightarrow BC=BA'+A'C \\
 & \Rightarrow BC=x+y \\
 & \Rightarrow BC=4\sqrt{3}+4 \\
 & \therefore BC=4\left( 1+\sqrt{3} \right)m \\
\end{align}\]
Hence, the width of the river is \[4\left( 1+\sqrt{3} \right)m\].

Note: The representation of the angle of depression plays an important role in this question. If we represent it as the angle of elevation then the answer changes completely.
We can also calculate the width of the river from the distance AA" which also gives the same result because the lines are parallel then the angles required for the calculation will be \[{{30}^{\circ }}\] and \[{{45}^{\circ }}\] only. So, this also gives the same result.
While substituting the values we need to substitute the corresponding values only or else the answer changes completely.