Question

From a circular disc of radius R and mass 3M, a small disc of mass M and radius $\dfrac{R}{3}$ is removed concentrically. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is
A. $\dfrac{13}{9}M{{R}^{2}}$
B. $M{{R}^{2}}$
C. $4M{{R}^{2}}$
D. $\dfrac{4}{9}M{{R}^{2}}$

Answer 1

Hint: As a first step, you could recall the expression for the moment of inertia of a circular disc about the perpendicular axis passing through its center. Now you could apply this expression for the case of the complete disc before the removal of the smaller disc, then you could do the same for the removed disc. Their difference will give us the required answer.

Formula used:
Moment of inertia of a disc,
$I=\dfrac{1}{2}M{{R}^{2}}$

Complete answer:
In the question, we have a circular disc of radius R and mass 3M and a small part in the shape of disc of radius $\dfrac{R}{3}$ is removed from it concentrically. We are supposed to find the moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc passing through its centre.
Firstly, let us recall the moment of inertia of the disc about an axis perpendicular to passing through its centre,
$I=\dfrac{1}{2}M{{R}^{2}}$

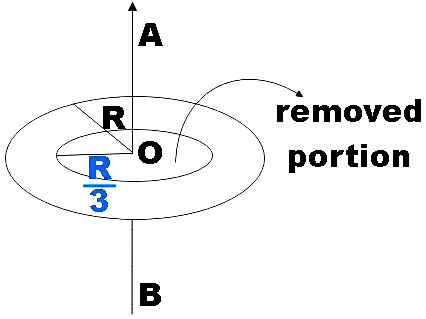
Now for the circular disc of radius R and mass 3M, the moment of inertia would be,
${{I}_{1}}=\dfrac{1}{2}\left( 3M \right){{R}^{2}}$ ……………………………………………….. (1)
For the circular disc that is being removed from this disc,
${{I}_{2}}=\dfrac{1}{2}M{{\left( \dfrac{R}{3} \right)}^{2}}=\dfrac{1}{18}M{{R}^{2}}$……………………………………… (2)
We know that subtracting equation (2) from equation (1) would give us the moment of inertia of the remaining portion of the disc after the removal of the smaller disc.
$I'={{I}_{1}}-{{I}_{2}}$
$\Rightarrow I'=\dfrac{3M{{R}^{2}}}{2}-\dfrac{M{{R}^{2}}}{18}$
$\Rightarrow I'=\dfrac{27M{{R}^{2}}-M{{R}^{2}}}{18}$
$\Rightarrow I'=\dfrac{26M{{R}^{2}}}{18}$
$\therefore I'=\dfrac{13M{{R}^{2}}}{9}$
Therefore, we found the moment of inertia of the remaining portion of the disc to be$\dfrac{13M{{R}^{2}}}{9}$.
Hence, option A is found to be the correct answer.

Note:
The answer would have been completely different if the smaller disc was not removed concentrically. Step followed in the solution would exactly be the same for the removal of the smaller disc non-concentrically. But the difference would be in the case of moment of inertia of the part being removed.