Question

From a circle of radius a, an isosceles right angle triangle with hypotenuse as the diameter of the circle is removed. The distance of center of gravity of the remaining position from the center of the circle is:
A. $3\left( {\pi - 1} \right)a$
B. $\dfrac{{\left( {\pi - 1} \right)a}}{6}$
C. $\dfrac{a}{{3\left( {\pi - 1} \right)}}$
D. $\dfrac{a}{{3\left( {\pi + 1} \right)}}$

Answer 1

Hint: First draw a diagram according to the statement given in the question. Using the formula for the center of gravity of the remaining body we can solve this problem. First calculate the mass of the circle and mass of the triangle around the origin then put this in the center of gravity formula.

Formula used:
We know the center of gravity of the remaining body is represented as,
$y = \dfrac{{{m_1}{r_1} - {m_2}{r_2}}}{{{m_1} - m}} $
Where, ${m_1} = $ Mass of the circle, ${m_2} = $ Mass of the triangle and ${r_{1\,\,\,,}}\,{r_2}$ are the distance of the circle and triangle respectively from the center of the centre of the circle.
Area of the triangle= $\dfrac{1}{2}bh$
Where, Base of the triangle = $b$ and Height of the triangle = $h$.

Complete step by step answer:
As per the problem there is a circle whose radius is a and an isosceles right angle triangle with hypotenuse as the diameter of the circle is removed.

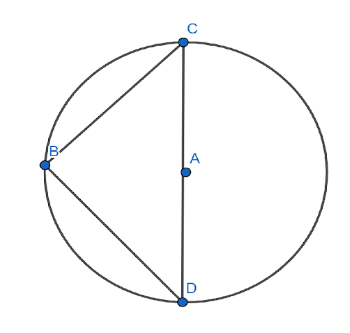
We need to calculate the distance of the center of gravity of the remaining position from the center of the circle. Let us assume a circle of radius a and an isosceles right angle triangle is removed from the circle whose diameter is equal to the hypotenuses of the triangle.
We know the center of gravity of the remaining body is represented as
$y = \dfrac{{{m_1}{r_1} - {m_2}{r_2}}}{{{m_1} - m}} \ldots \ldots \left( 1 \right)$

We know, mass of the body is represented as density of the body multiplied by its area.Mathematically,
$m = \rho A$
With the help this mass formula we can calculate the mass of the circle and triangle,
Area of the circle= $\pi \times $ radius of the circle
${m_1} = \rho \times \pi {a^2} \ldots \ldots \left( 2 \right)$
Area of the triangle= $\dfrac{1}{2}bh$
Where, Base of the triangle = $b$ and Height of the triangle = $h$
${m_2} = \rho \times \dfrac{1}{2} \times 2a \times a$
Solving it further,
${m_2} = \rho {a^2} \ldots \ldots \left( 3 \right)$

Here density of the body is same for both circle and triangle as both are made up of same particles.
Putting equation $\left( 2 \right)$ and $\left( 3 \right)$ in equation $\left( 1 \right)$ we get,
$y = \dfrac{{\rho \pi {a^2}{r_1} - \rho {a^2}{r_2}}}{{\rho \pi {a^2} - \rho {a^2}}}$
${r_1} = $ distance of the genter gravity of the circle from the centre of the circle $ = 0$
${r_2} = $ distance of the center of gravity of the triangle from the center of circle $ = - \dfrac{a}{3}$
${r_2}$ is negative as we take the radius in negative x-axis

Putting this in the above equation we get,
$y = \dfrac{{\rho \pi {a^2}\left( 0 \right) - \rho {a^2}\left( { - \dfrac{a}{3}} \right)}}{{\rho \pi {a^2} - \rho {a^2}}}$
$ \Rightarrow y = \dfrac{{ - \rho {a^2}\left( { - \dfrac{a}{3}} \right)}}{{\rho \pi {a^2} - \rho {a^2}}}$
$ \Rightarrow y = \dfrac{{\rho {a^2}\left( {\dfrac{a}{3}} \right)}}{{\rho \pi {a^2} - \rho {a^2}}}$
Cancelling the common term from numerator and denominator,
$y = \dfrac{{{a^2}\left( {\dfrac{a}{3}} \right)}}{{\pi {a^2} - {a^2}}}$
$ \Rightarrow y = \dfrac{{\dfrac{{{a^3}}}{3}}}{{{a^2}\left( {\pi - 1} \right)}}$
$ \therefore y = \dfrac{a}{{3\left( {\pi - 1} \right)}}$

Therefore the correct option is $\left( C \right)$.

Note: Always keep in mind the density of both circle and triangle will be the same because both come from the same body. Remember that the center of a triangle is one third of its height from the base of the triangle and the center of the circle coincides with its center itself.