Question

From a boat 300 metres away from a vertical cliff, the angles of elevation of the top and the foot of a vertical concrete pillar at the edge of the cliff are $ 55{}^\circ 4{0}' $ and $ 54{}^\circ 2{0}' $ respectively. Find the height of the pillar correct to the nearest meter.

Answer 1

Hint: We will label the points in the diagram and label the angles of elevation given. We will convert the degrees and minutes into decimal degrees. For this, we will divide the minutes by 60 and add the obtained decimal number to the degrees. Then we will take the tan values of both the angles. We will get the height of the cliff and the height of the cliff and pillar. We will use this information to find the height of the pillar.

Complete step by step answer:
We will label the points in the diagram given and also mark the angles of elevation. The angles of elevation of the top and the foot of a vertical concrete pillar at the edge of the cliff are $ 55{}^\circ 4{0}' $ and $ 54{}^\circ 2{0}' $ respectively. Then, the figure looks like the following,

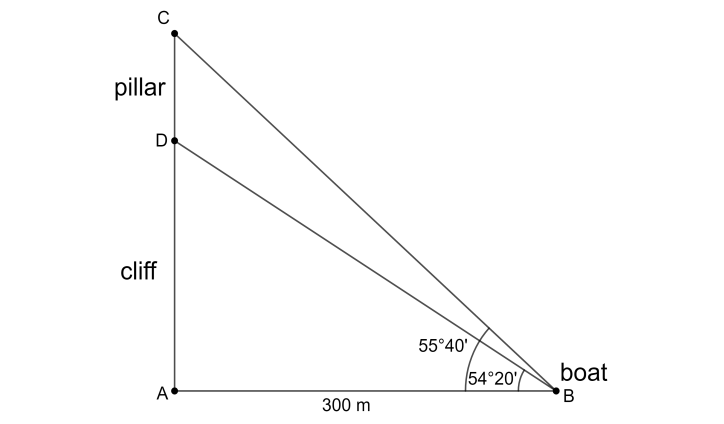
Let us convert the degrees and minutes into decimal degrees. We will divide the minutes by 60 to obtain the decimal equivalent for it. So, we have the following,
 $ \begin{align}
  & 54{}^\circ 2{0}'=54{}^\circ +\dfrac{20}{60} \\
 & \Rightarrow 54{}^\circ 2{0}'=54{}^\circ +0.33{}^\circ \\
 & \therefore 54{}^\circ 2{0}'=54.33{}^\circ \\
\end{align} $
Similarly, we have
 $ \begin{align}
  & 55{}^\circ 4{0}'=55{}^\circ +\dfrac{40}{60} \\
 & \Rightarrow 55{}^\circ 4{0}'=55{}^\circ +0.67{}^\circ \\
 & \therefore 55{}^\circ 4{0}'=55.67{}^\circ \\
\end{align} $
From the figure, we can see that segment AC is perpendicular to segment AB. We know that $ \tan \theta =\dfrac{\text{Opposite}}{\text{Adjacent}} $ . Now, in $ \Delta \text{ABD} $ , we will look at the following trigonometric ratio,
 $ \tan 54.33{}^\circ =\dfrac{\text{AD}}{\text{AB}} $
Therefore, we have
 $ \begin{align}
  & \text{AD}=\text{AB}\times \tan 54.33{}^\circ \\
 & \Rightarrow \text{AD}=300\times 1.39 \\
 & \therefore \text{AD}=417\text{ m} \\
\end{align} $
Next, we will consider $ \Delta \text{ABC} $ . We will consider the following trigonometric ratio,
 $ \begin{align}
  & \tan 55.67{}^\circ =\dfrac{\text{AC}}{\text{AB}} \\
 & \Rightarrow \text{AC}=\text{AB}\times \text{tan55}\text{.67}{}^\circ \\
 & \Rightarrow \text{AC}=300\times 1.46 \\
 & \therefore \text{AC}=438\text{ m} \\
\end{align} $
We have to find the height of the pillar, which is $ \text{AC}-\text{AD}=438-417=21\text{ m} $ . So, the height of the pillar is 21 metres.

Note:
 It is important to have a figure with the given information for such types of questions. We should be familiar with the trigonometric functions and their definitions. We should know that 1 degree is equivalent to 60 minutes. So, we divide the minutes by 60 to obtain the measurement in degrees. The conversion from degrees and minutes to decimal degrees is essential for calculations.