Question

What is the fraction of each of the shaded parts?

Answer 1

Hint: We need to find the fraction of each of the shaded parts. We start to solve the question by finding out the number of shaded portions and the total number of portions of each figure. Then, the ratio of the number of shaded portions to the total number of portions to get the desired result.

Complete step-by-step solution:
We are given a few figures and are asked to find the fraction of each of the shaded parts. We will be solving the given question by finding out the ratio of the number of shaded portions to the total number of portions.
A fraction, in mathematics, represents a part of a whole thing. It consists of two parts namely,
numerator, denominator.
The number on the top is called the numerator.
The number on the bottom is called the denominator.
Let us understand the concept of the fraction with an example as follows,
Example:
$\Rightarrow \dfrac{a}{b}$
In the above fraction,
$a$ is the numerator of the fraction
$b$ is the denominator of the fraction
According to the question,
We need to find the fraction of each of the shaded parts.

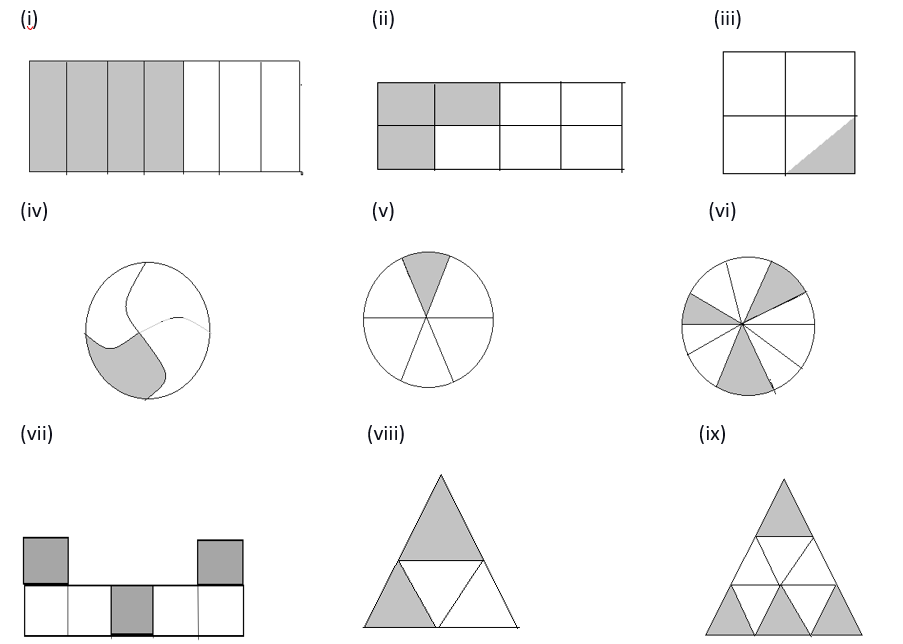
(i)

In the above figure,
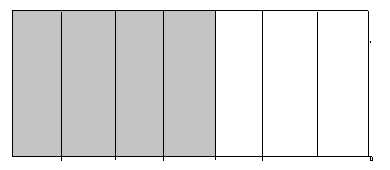
The total number of portions is equal to 7.
The number of shaded portions is equal to 4.
The fraction of each of the shaded parts is given as follows,
$\Rightarrow \dfrac{\text{number of shaded portions}}{\text{total number of portions}}$
Substituting the values, we get,
$\Rightarrow \dfrac{4}{7}$
(ii)
   

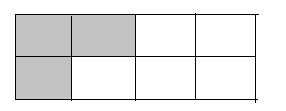
In the above figure,
The total number of portions is equal to 8.
The number of shaded portions is equal to 3.
The fraction of each of the shaded parts is given as follows,
$\Rightarrow \dfrac{\text{number of shaded portions}}{\text{total number of portions}}$
Substituting the values, we get,
$\Rightarrow \dfrac{3}{8}$
(iii)
   

In the above figure,
The total number of triangles formed in the above figure is 8. So, the total number of portions is equal to 8.
The number of shaded portions is equal to 1.
The fraction of each of the shaded parts is given as follows,
$\Rightarrow \dfrac{\text{number of shaded portions}}{\text{total number of portions}}$
Substituting the values, we get,
$\Rightarrow \dfrac{1}{8}$

(iv)

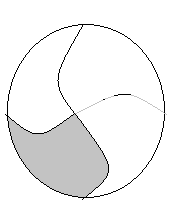
In the above figure,
The total number of portions is equal to 4.
The number of shaded portions is equal to 1.
The fraction of each of the shaded parts is given as follows,
$\Rightarrow \dfrac{\text{number of shaded portions}}{\text{total number of portions}}$
Substituting the values, we get,
$\Rightarrow \dfrac{1}{4}$
(v)
        

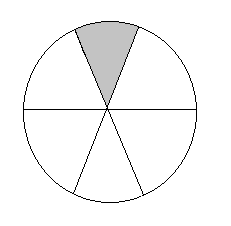
In the above figure,
The total number of portions is equal to 6.
The number of shaded portions is equal to 1.
The fraction of each of the shaded parts is given as follows,
$\Rightarrow \dfrac{\text{number of shaded portions}}{\text{total number of portions}}$
Substituting the values, we get,
$\Rightarrow \dfrac{1}{6}$
(vi)
      

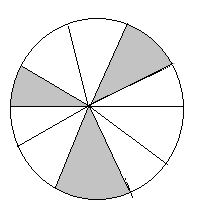
In the above figure,
The total number of portions is equal to 10.
The number of shaded portions is equal to 3.
The fraction of each of the shaded parts is given as follows,
$\Rightarrow \dfrac{\text{number of shaded portions}}{\text{total number of portions}}$
Substituting the values, we get,
$\Rightarrow \dfrac{3}{10}$

(vii)

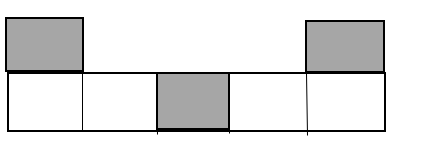
In the above figure,
The total number of portions is equal to 7.
The number of shaded portions is equal to 3.
The fraction of each of the shaded parts is given as follows,
$\Rightarrow \dfrac{\text{number of shaded portions}}{\text{total number of portions}}$
Substituting the values, we get,
$\Rightarrow \dfrac{3}{7}$
(viii)

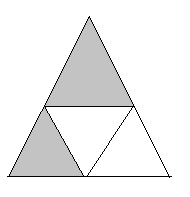
In the above figure,
The total number of portions is equal to 4.
The number of shaded portions is equal to 2.
The fraction of each of the shaded parts is given as follows,
$\Rightarrow \dfrac{\text{number of shaded portions}}{\text{total number of portions}}$
Substituting the values, we get,
$\Rightarrow \dfrac{2}{4}$
(ix)

In the above figure,
The total number of portions is equal to 9.
The number of shaded portions is equal to 4.
The fraction of each of the shaded parts is given as follows,
$\Rightarrow \dfrac{\text{number of shaded portions}}{\text{total number of portions}}$
Substituting the values, we get,
$\Rightarrow \dfrac{4}{9}$

Note: The given question is a direct formula based and any mistake in writing the formula to find the fraction of each shaded part will result in an incorrect solution. We must be careful while counting the total number of portions and the number of shaded portions in the figure to get precise results.