Question

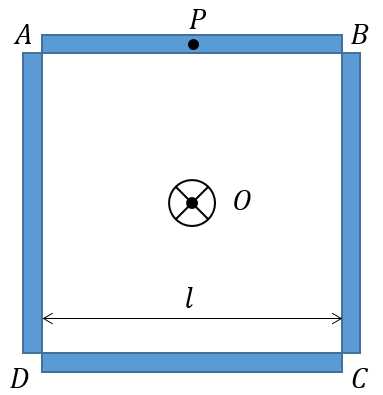
Four thin rods of same mass $M$ and same length $l$ form a square as shown in the figure. Moment of inertia of this system about an axis passing through center $O$ and perpendicular to plane is:

Answer 1

Hint: Moment of inertia is the rotational analog of mass. Moment of inertia is measured by taking the second moment of mass with respect to distance from an axis. It helps us to determine the torque required for producing a given angular acceleration.

Formula used:
${I_{CM}} = \dfrac{1}{{12}}M{l^2}$ ,where ${I_{CM}}$ is the moment of inertia of the rod having length $l$ about an axis parallel to the center of gravity
$I = {I_{CM}} + M{X^2}$, where $I$ is the moment of inertia about axis passing through $O$, where ${I_{CM}}$ is the moment of inertia of the rod about an axis parallel to the center of gravity, $M$ is the mass of the body and $X$ is the distance between the axes.

Complete step-by-step solution -
Moment of inertia of the center of square ABCD from the axis passing through $O$ can be found out by using parallel axis theorem and symmetry.
${I_{CM}} = \dfrac{1}{{12}}M{l^2}$, where ${I_{CM}}$ is the moment of inertia of the rod having length $l$about an axis parallel to the center of gravity. The distance between both the axes i.e., from the axis passing through point P and that through O is $\dfrac{l}{2}$. Substituting these in the equation $I = {I_{CM}} + M{X^2}$, we get the moment of inertia one uniform rod ${I_1}$
${I_1} = \dfrac{1}{{12}}M{l^2} + M{(\dfrac{l}{2})^2}$

${I_1} = \dfrac{1}{{12}}M{l^2} + \dfrac{1}{4}M{l^2}$
${I_1} = M{l^2}(\dfrac{1}{{12}} + \dfrac{1}{4})$
${I_1} = (\dfrac{1}{3})M{l^2}$
Remember this is for one rod. There are four identical uniform rods in the figure. Therefore using symmetry the net moment of inertia is ${I_{net}} = 4 \times {I_1}$
${I_{net}} = \dfrac{4}{3}M{l^2}$

Additional Information:
Parallel Axis Theorem: The moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis through its center of gravity and the product of the mass of the body and the square of the distance between the two axes.
Perpendicular Axis theorem: The moment of inertia of a plane laminar body about an axis perpendicular to the plane is equal to the sum of the moments of inertia about two mutually perpendicular axes in the plane of the lamina such that the three mutually perpendicular axes have a common point of intersection.

Note: As the axis of rotation changes, the moment of inertia changes. Using parallel and perpendicular axis theorem we can find the moment of inertia of any axis if we know the moment of inertia about a parallel axis through its center of gravity.