Question

Four particles having a mass $ m $ , $ 2m $ , $ 3m $ and $ 4m $ are placed at the four corners of a square of edge ‘a’. Find the gravitational force acting on a particle of mass $ m $ placed at the center.

Answer 1

Hint To solve this question, we need to use the formula of Newton's law of gravitation. Then, we have to calculate the gravitational force on the center particle due to each mass. Vector addition of these forces will give the final answer.

Formula Used: The formula used in this solution is given as
 $ F = G\dfrac{{{m_1}{m_2}}}{{{r^2}}} $
Here, $ F $ is the Gravitational force between two bodies of masses $ {m_1} $ and $ {m_2} $ respectively, separated by a distance of $ r $ units. Here $ G $ is the Universal Gravitational Constant.

Complete step by step answer
Let us first try to understand the conditions given in the question by drawing a figure.

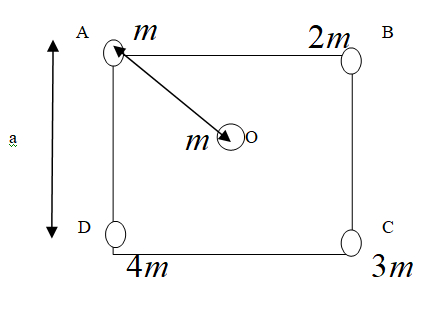
Now, using the Pythagoras theorem let us first calculate the distance OA. In order to do that let us first consider a point P that divides the line segment AD into 2 equal parts.

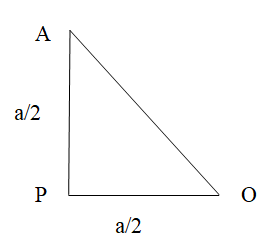
So now using the Pythagoras theorem, we get,
 $\Rightarrow A{O^2} = A{P^2} + P{O^2} $
This gives us,
 $ \Rightarrow
  AO = \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} \\
   \Rightarrow AO = \dfrac{a}{{\sqrt 2 }} \\
 $
Now, let us try to resolve the forces acting on the mass $ m $ at O

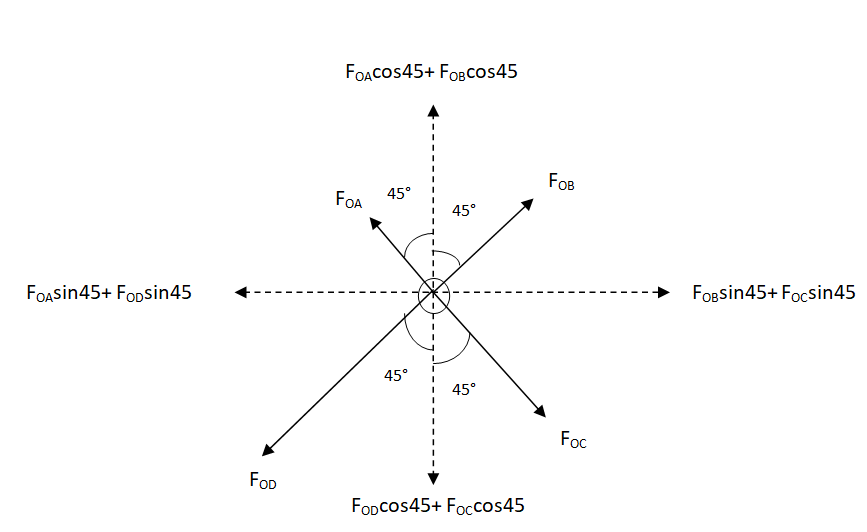
Now, from the formula for the force of gravitation, let us calculate the forces as,
 $
\Rightarrow {F_{OA}} = G\dfrac{{m.{m_{}}}}{{{{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}^2}}} \\
   \Rightarrow {F_{OA}} = G\dfrac{{{m^2}}}{{\left( {\dfrac{{{a^2}}}{2}} \right)}} \\
 $
This gives,
 $\Rightarrow {F_{OA}} = G\dfrac{{2{m^2}}}{{{a^2}}} $
Similarly, we get,
 $\Rightarrow {F_{OB}} = G\dfrac{{4{m^2}}}{{{a^2}}} $ , $ {F_{OC}} = G\dfrac{{6{m^2}}}{{{a^2}}} $ and $ {F_{OD}} = G\dfrac{{8{m^2}}}{{{a^2}}} $
Now we calculate the horizontal components and vertical components.
 $ \Rightarrow
  {F_{left}} = {F_{OA}}sin45 + {\text{ }}{F_{OD}}sin45 \\
   \Rightarrow {F_{left}} = \left( {\dfrac{{2G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) + \left( {\dfrac{{8G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) \\
 $
This gives us,
 $\Rightarrow {F_{left}} = \left( {\dfrac{{10G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) $
Similarly, we get,
 $ \Rightarrow
  {F_{right}} = {F_{OB}}sin45 + {\text{ }}{F_{OC}}sin45 \\
   \Rightarrow {F_{right}} = \left( {\dfrac{{4G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) + \left( {\dfrac{{6G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) = \left( {\dfrac{{10G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) \\
 $
Thus, we find that, $ {F_{left}} = {F_{right}} $
Hence, the horizontal component gets cancelled. Now let us calculate the vertical component as,
 $ \Rightarrow
  {F_{up}} = {F_{OA}}\cos 45 + {\text{ }}{F_{OB}}\cos 45 \\
   \Rightarrow {F_{up}} = \left( {\dfrac{{2G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) + \left( {\dfrac{{4G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) = \left( {\dfrac{{6G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) \\
 $
Similarly,
 $ \Rightarrow
  {F_{down}} = {F_{OC}}\cos 45 + {\text{ }}{F_{OD}}\cos 45 \\
   \Rightarrow {F_{down}} = \left( {\dfrac{{6G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) + \left( {\dfrac{{8G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) = \left( {\dfrac{{14G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) \\
 $
Thus, we get the net force acting at the particle at O to be,
 $\Rightarrow {F_{net}} = {F_{down}} - {F_{up}} \\
   \Rightarrow {F_{net}} = \left( {\dfrac{{14G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) - \left( {\dfrac{{6G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right) \\
 $
Thus we get,
 $\Rightarrow {F_{net}} = \left( {\dfrac{{8G{m^2}}}{{{a^2}}}} \right)\left( {\dfrac{1}{{\sqrt 2 }}} \right)N \\
   \Rightarrow {F_{net}} = \left( {\dfrac{{4\sqrt 2 G{m^2}}}{{{a^2}}}} \right)N \\
 $
$ \therefore $ The net force acting on the particle at the center is in the downward direction and its value is $ \left( {\dfrac{{4\sqrt 2 G{m^2}}}{{{a^2}}}} \right)N $ /.

Note
Do not add the forces algebraically. Always remember that the force is a vector quantity. So, the vector addition is necessary to obtain the net force. Apart from calculating the net force by taking components, we could have also done this using parallelogram law. For that we would need to obtain the resultant forces along the diagonals of the given square. Then the vector addition of these forces using the parallelogram law would yield the final answer.