Question

Four pairs showing measurement of sides $ \overline {AB} ,\overline {BC} $ and $ \overline {CA} $ of $ \Delta ABC $ are given below. Show which of the following pair/s is/are shows a right angle triangle.
Pair $ P:AB = 25 $ $ BC = 7 $ $ AC = 24 $
Pair $ Q:AB = 8 $ $ BC = 6 $ $ AC = 10 $
Pair $ R:AB = 3 $ $ BC = 4 $ $ AC = 6 $
Pair $ S:AB = 8 $ $ BC = 6 $ $ AC = 5 $
 $ \left( A \right) $ Pairs $ Q $ and $ R $ show a right angle triangle.
 $ \left( B \right) $ Pairs $ P $ and $ Q $ show a right angle triangle.
 $ \left( C \right) $ Pairs $ P $ and $ S $ show a right angle triangle.
 $ \left( D \right) $ Pairs $ P,Q $ and $ S $ show a right angle triangle.

Answer 1

Hint: $ \Rightarrow $ In these types of problems, we have to find either sides of a right angle triangle or angles of a triangle.
 $ \Rightarrow $ Here, we have to find which sides of the triangle form the right angle triangle. For which we will be using Pythagoras theorem.

Complete step-by-step answer:
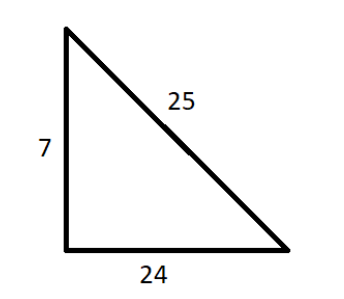
So, starting with pair $ P $ ,
 $ \Rightarrow A{C^2} + B{C^2} = {24^2} + {7^2} = 576 + 49 = 625 = {25^2} $
 $ A{B^2} = {25^2} $
Therefore, $ A{B^2} = A{C^2} + B{C^2} $

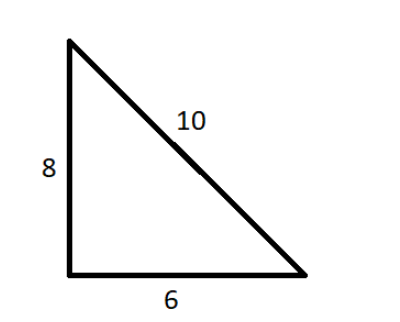
Now, For Pair $ Q $ ,
 $ \Rightarrow A{B^2} + B{C^2} = {8^2} + {6^2} = 64 + 36 = 100 = {10^2} $
 $ A{C^2} = {10^2} $
Therefore, $ A{B^2} + B{C^2} = A{C^2} $

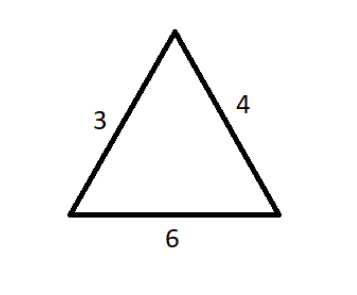
Now, For Pair $ R $ ,
 $ \Rightarrow A{B^2} + B{C^2} = {3^2} + {4^2} = 9 + 16 = 25 = {5^2} $
 $ A{C^2} = {6^2} $
Therefore, $ A{B^2} + B{C^2} \ne A{C^2} $

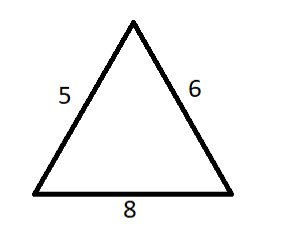
Now, For Pair $ S $ ,
 $ \Rightarrow A{C^2} + B{C^2} = {5^2} + {6^2} = 25 + 36 = 61 $
 $ A{B^2} = {8^2} $
Therefore, $ A{B^2} \ne A{C^2} + B{C^2} $
Therefore Pairs $ P $ and $ Q $ show a right angle triangle.

Therefore Pairs $ P $ and $ Q $ show a right angle triangle.
So, the correct answer is “Option B”.

Note: The Pythagorean Theorem tells how the lengths of the three sides of a right triangle relate to each other. It states that in any right triangle, the sum of the squares of the two legs equals the square of the hypotenuse. Remember that a right triangle has a $ 90^\circ $ angle, which we usually mark with a small square in the corner. The side of the triangle opposite the $ 90^\circ $ angle is called the hypotenuse, and the other two sides are called the legs.