Question

Four $ \left[ {40{\text{W}},{\text{ }}230{\text{V}}} \right] $ bulbs are connected to a $ 230{\text{V}} $ supply as shown below.
-Which are the bulbs connected in series?
-Which are the bulbs that can work at $ 40{\text{W}} $ power?
-Write two advantages of connecting household equipment in parallel.

Answer 1

Hint:
To answer this question, we need to use the bulb rating given to find the resistance of each bulb using its relation with the power. For identifying the series and the parallel combinations, we have to see the connection of the terminals of the bulbs. After identifying the series and the parallel combinations, we can divide the voltage across each bulb to find out the maximum power.
Formula Used: The formula used in this solution is
 $ P = \dfrac{{{V^2}}}{R} $ , here $ P $ is the power developed across a resistance $ R $ , which is supplied to a voltage $ V $

Complete step by step answer:
Let the resistance of the bulbs be $ R $ .
The ratings of each of the four bulbs in the given circuit of the question are
Maximum power $ P = 40{\text{W}} $
Voltage $ V = 230{\text{V}} $
We know that the power is given by
 $ P = \dfrac{{{V^2}}}{R} $
So the resistance is given by
 $ R = \dfrac{{{V^2}}}{P} $
Putting the values from the rating of the bulb, we get
 $ R = \dfrac{{{{230}^2}}}{{40}} $
 $ R = 1322.5\Omega $
So the resistance of each bulb is equal to $ 1322.5\Omega $ .
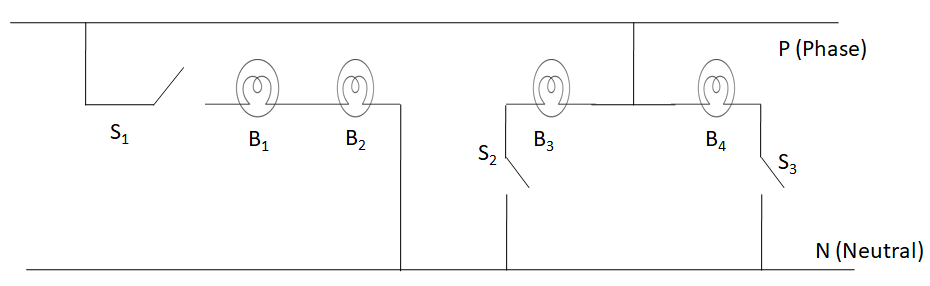
-We can see that the bulbs $B_1$ and $B_2$ connected through the switch S1 have one terminal common. The other terminal of bulb $B_1$ is connected to the phase line, while that of the bulb $B_2$ is connected to the neutral line. So, the bulbs $B_1$ and $B_2$ are connected in series between the phase and the neutral.
Hence, the answer to this part is $B_1$ and $B_2$.
-Considering the bulbs $B_1$ and $B_2$, as they are connected in series, the $ 230{\text{V}} $ of the supply is divided between them. The voltage is equally divided, as both the bulbs have the same resistance. So, the voltage across each bulb is
 $ {V_1} = \dfrac{{230}}{2} = 115{\text{V}} $ . So the maximum power across each of the bulbs $B_1$ and $B_2$ is given by $ {P_1} = \dfrac{{{{115}^2}}}{{1322.5}} = 10{\text{W}} $
Therefore, the maximum power which the bulbs $B_1$ and $B_2$ can withstand is equal to $ 10{\text{W}} $ . So they cannot work at $ 40{\text{W}} $ power.
Now, considering the bulbs $B_3$ and $B_4$, we can see that in both of them, one terminal is connected to the phase and the other to the neutral. Hence, they are connected in parallel. We know that the voltage is not divided in a parallel combination. So, the voltage across both of them is
 $ {V_2} = 230{\text{V}} $
So the maximum power across each of the bulbs $B_3$ and $B_4$ is given by
 $ {P_2} = \dfrac{{{{230}^2}}}{{1322.5}} = 40{\text{W}} $ .
Therefore, the bulbs $B_3$ and $B_4$ can work at $ 40{\text{W}} $ power.
Hence, the answer of this part is $B_3$ and $B_4$.
-As can be seen in b part, the parallel combination does not divide the voltage across each element. Hence, each device can work on its maximum power rating, when connected in a parallel combination with the other devices.
Also, in a series combination, if one of the elements stops working, the other elements stop working. This is because the circuit breaks at the defective element and the current stops flowing. But in a parallel combination, the current is divided among the devices. Hence, if one device stops working, the other devices are not affected.

Note:
As all the four bulbs in this question are identical, we can attempt this question without even finding the value of resistance. We can use the proportionality between the power and the voltage to directly evaluate the maximum power across each bulb.