Question

Four horses are tethered at four corners of a square field of side 70 meters so that they cannot reach one another. The area left ungrazed by the horses is-
(A). 1050 sq m
(B). 3850 sq m
(C). 950 sq m
(D). 1075 sq m

Answer 1

Hint: This is a problem of area and mensuration. We will first find the areas of quarter circles grazed by each of the horses and then subtract it from the area of the square field to find the area of the ungrazed region. One needs to know the formulas for the area of a square and the circle, which are given by-
$Area\left( {square} \right) = side \times side$
$Area\left( {circle} \right) = \pi {r^2}$

Complete step-by-step answer:
Let ABCD be the square field. The horses are tethered at ABCD. They just cannot reach each other, so the radius of each rope should be exactly half of the side of the lawn. The four quarter circles represent the area grazed by each horse. The middle region left is the area ungrazed.

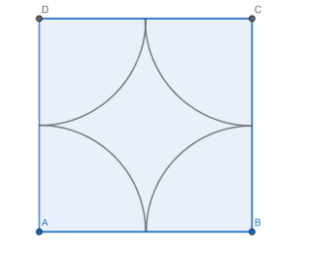
The area of square field =$70 \times 70 = 4900\;sq\;m$
The area of each quarter circle is $\dfrac{1}{4}$ of the area of a full circle. There are four quarter circles, hence their total area will be equal to the area of a complete circle.
Radius of the circle = 35 m
Area of the circle = $\pi {r^2} = 3.14 \times 35 \times 35 = 3846.5\;sq\;{\text{m}}$

Now we have to find the area of the ungrazed region. This area is given by-
= Area of square - Area of circle
$= 4900 - 3846.5$
$= 1053.5 $sq m
$= 1050$ sq m approx.

Hence the correct option is A. 1050 sq m

Note:It is important to read the question carefully. Students mark the answer as B because it is the grazed region, which is wrong. Also, students should never forget to mention the units in the final answer. If the accurate answer is not mentioned in the options, then best practice is to mark the closest answer. Students in a hurry often forget to multiply the area grazed by one horse by 4, which should be avoided.