Question

four equal charges of value \[+Q\] are placed at any four vertices of a regular hexagon of side ‘a’. By choosing the vertices, what can be the maximum possible magnitude of the electric field at the centre of the hexagon?
A. $\dfrac{Q}{4\pi {{\varepsilon }_{0}}{{a}^{2}}}$
B. $\dfrac{\sqrt{2}Q}{4\pi {{\varepsilon }_{0}}{{a}^{2}}}$
C. $\dfrac{\sqrt{3}Q}{4\pi {{\varepsilon }_{0}}{{a}^{2}}}$
D. $\dfrac{2Q}{4\pi {{\varepsilon }_{0}}{{a}^{2}}}$

Answer 1

Hint:-To get maximum possible magnitude of electric field at the centre of hexagon. We arrange four equal charges of value $\left( +Q \right)$ in series, then due to two charges, the horizontal component of the electric field is added and the vertical component is canceled out.

Complete step by step answer:
When four charges of magnitude $\left( +Q \right)$ are placed in such a way as shown in figure
  

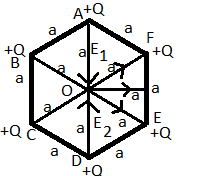
Let us consider a regular hexagon ABCDEF and four $\left( +Q \right)$ charges situated at point A, B, C, and D respectively.
Electric field formula due to a point charge $E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{r}^{2}}}$
Where $Q$ is the charge and $r$ is the distance between the charge and the point at which the field is found.
All the triangles are equilateral triangles, so the electric field at O due to charge $\left( +Q \right)$ at point A.
${{E}_{1}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{a}^{2}}}$ ……………………(1)
The electric field at O due to charge $\left( +Q \right)$ at point B .
${{E}_{2}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{a}^{2}}}$ ……………………….(2)
The electric field at O due to charge $\left( +Q \right)$ at point C .
${{E}_{3}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{a}^{2}}}$ ……………………………….(3)
The electric field at O due to charge $\left( +Q \right)$ at point D .
${{E}_{4}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{a}^{2}}}$ ……………………………(4)
From equation (1) and equation (4)
The magnitude of ${{E}_{1}}$ and ${{E}_{4}}$ are the same but direction is opposite to each other, so the resultant electric field of both are zero.
But from equation (2) and (3)
The magnitude of ${{E}_{2}}$ and ${{E}_{3}}$ are the same, but its horizontal components are added and the vertical component cancels out.
So resultant electric field is
  $E={{E}_{2}}\cos 45{}^\circ +{{E}_{3}}\cos 45{}^\circ $
 $\begin{align}
  & E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{a}^{2}}}\cos {{45}^{{}^\circ }}+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{a}^{2}}}\cos 45{}^\circ \\
 & E=\dfrac{Q}{4\pi {{\varepsilon }_{0}}{{a}^{2}}}\left[ \dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}} \right] \\
 & E=\dfrac{\sqrt{2}Q}{4\pi {{\varepsilon }_{0}}{{a}^{2}}} \\
\end{align}$

Note:
When the student calculate the resultant electric field the term cos45 has left many times, so carefully use the formula with all terms