Question

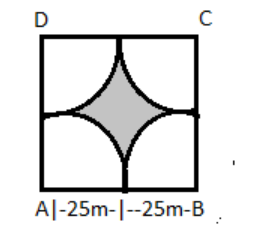
Four cows are tethered at four corners of a square plot of side $ 50\;m $ as shown in figure. What area will be left ungrazed?

Answer 1

Hint: Here we are asked to find out the area of the shaded part. So, we will first find the area of the square and the use area of the circle. As we can observe that the curved area is one fourth the area of the circle so apply the formula accordingly. Then will subtract the area of the curved path from the square area for the required area.

Complete step-by-step answer:
Let us assume that the length of the square be $ = l $
 $ l = 50m $ (Given)
We know that area of the square is $ = l \times l $
Place the values in the above equation –
 $ \Rightarrow A = 50 \times 50 $
Simplify the above equation –
 $ \Rightarrow A = 2500\;{m^2} $ .... (a)
Area of the quadrant inside the square is one fourth the area of the circle.
So, it can be represented as –
Area $ = \dfrac{1}{4}\pi {r^2} $
Also, radius $ r = 25\;m $ and $ \pi = \dfrac{{22}}{7} $ place the values in the above equation –
Area $ = \dfrac{1}{4} \times \dfrac{{22}}{7} \times {(25)^2} $
Simplify the above equation –
Area $ = 491.70\;{m^2} $ ... (B)
Now, the area of the shaded region $ = $ Area of square $ - 4 \times $ Area of the quadrant
Place values from the equation (A) and (B)
The area of the shaded region $ = 2500 - 4(491.07) $
Simplify the above equation –
The area of the shaded region $ = 2500 - 1964.28 $
Do subtraction –
The area of the shaded region $ = 535.71\;{m^2} $
Hence, the area of $ 535.71\;{m^2} $ will be left ungrazed.
So, the correct answer is “$ 535.71\;{m^2} $”.

Note: Always observe the given figure properly and then apply the correct formula. Be good in squares of the numbers and its concept. When you find the area, the respective units given in meter becomes meter square, centimetre will become centimetre square. Do not forget to write the appropriate unit in the final answer.