Question

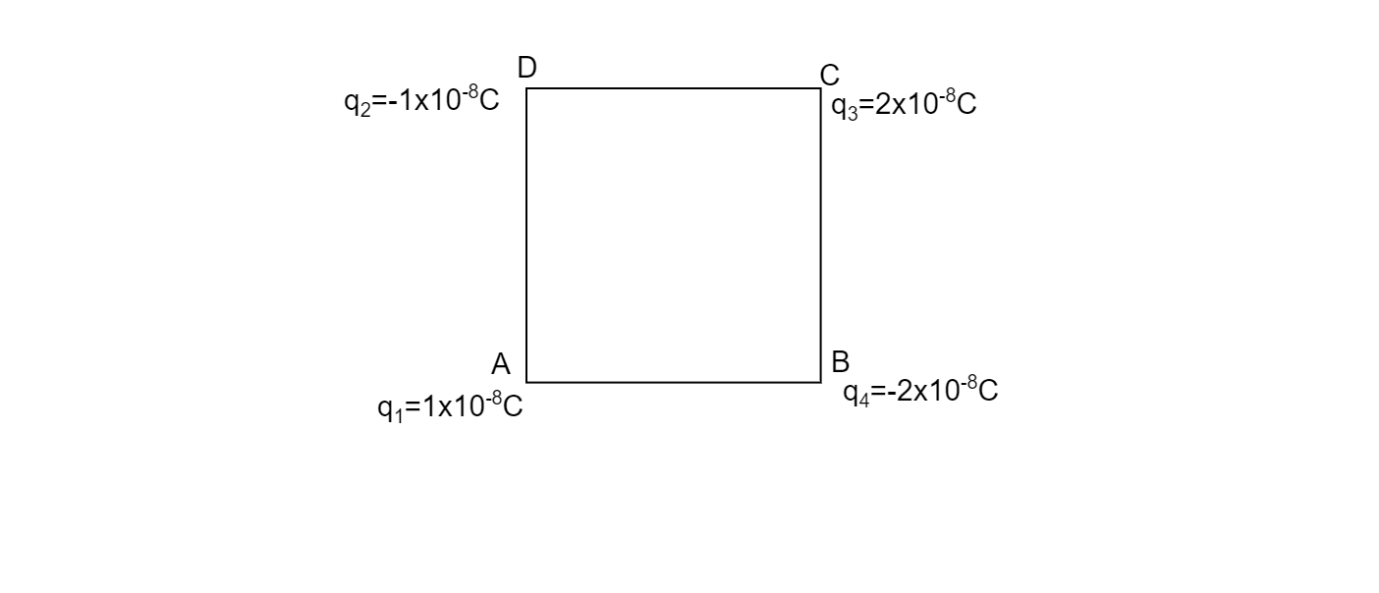
Four charges are placed at the vertices of square with side of $5cm$ . The charges are: $1, - 1,2, - 2 \times {10^{ - 8}}C$ . What is the Electric field at the center of the square?

Answer 1

Hint: First let’s see the top left corner charge and right bottom corner charge i.e. ${q_2}$ and ${q_4}$ . since it’s a square both of them are at equal distance from the center. find the net field at the center, similar way for a charge at the top right corner and bottom left corner i.e. ${q_1}$ and ${q_3}$ . find the distance of separation, then find field magnitude, then calculate the electric field at the center of the square.

Complete answer:

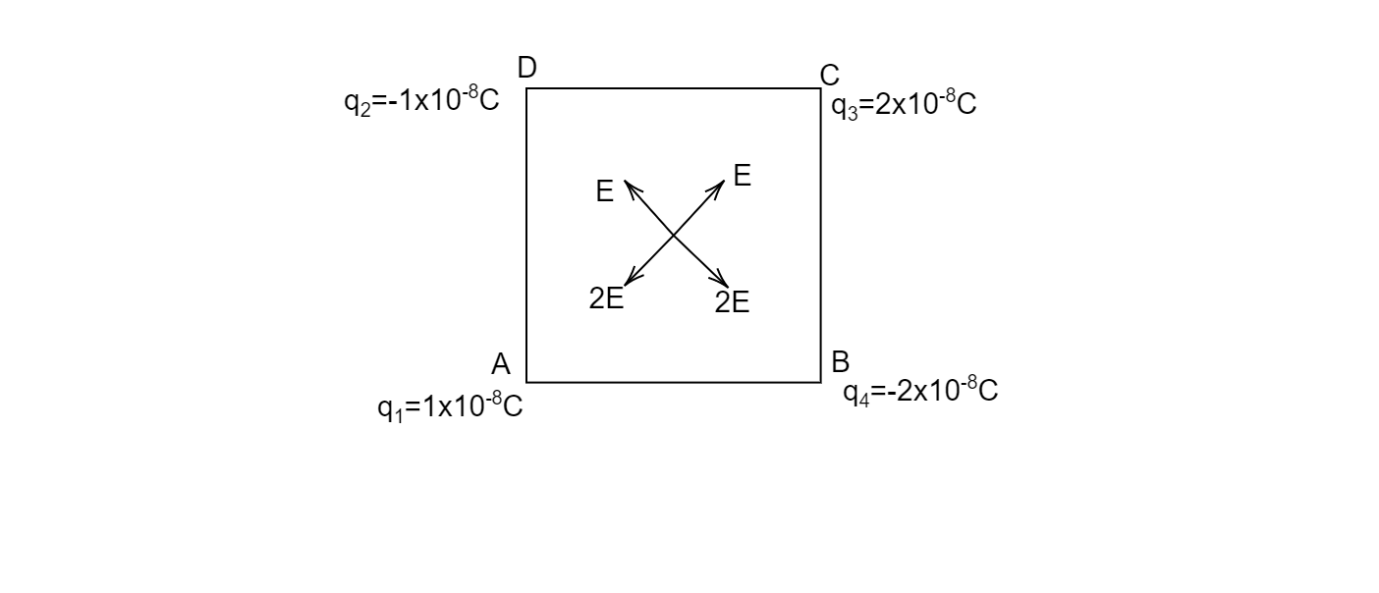
At point, A due to charge ${q_1}$ the electric field is away from the charge because it's positive so it will create repulsive force let it be $E$ , due to charge ${q_2}$ the electric field is towards the charge because it's negative let it be $E$.
Similarly, for charge ${q_3}$ the electric field is away from the charge, the charge has doubled but the distance is same from the center let it be $2E$, at last for charge ${q_4}$ the electric field is towards the charge let it also be $2E$
Now we see the charge ${q_1}$ and ${q_3}$ are linear and in the opposite direction so the net electric field will be $ \Rightarrow 2E - E = E$
Similarly for ${q_2}$ and ${q_4}$ .

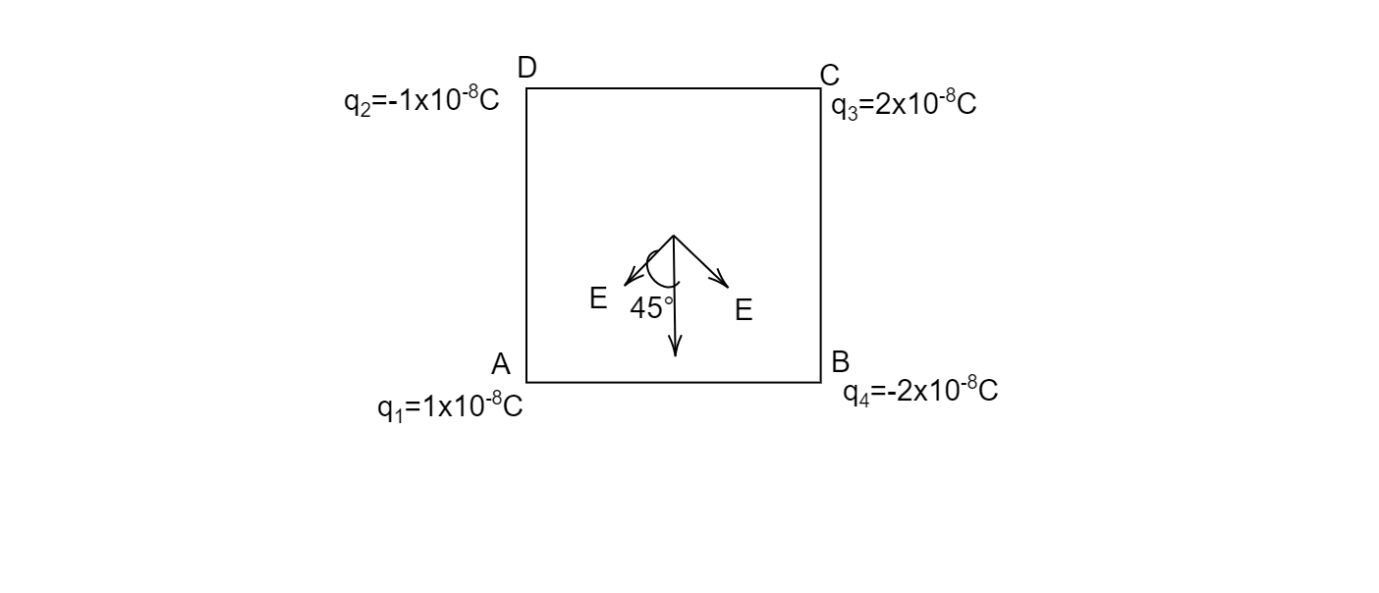
From the above diagram, both the electric field are perpendicular to each other so the net electric field will be in between
$ \Rightarrow {E_{net}} = \sqrt {{E^2} + {E^2}} $
Hence, ${E_{net}} = E\sqrt 2 $
Now finding the value of $E$
$ \Rightarrow E = \dfrac{{kq}}{{{{\left( {halfofdiagonal} \right)}^2}}}$
$ \Rightarrow E = \dfrac{{kq}}{{{{\left( r \right)}^2}}}$
Now we will find the distance of separation $r$ , diagonal is $a\sqrt 2 $ so,
$ \Rightarrow r = \dfrac{a}{2}\sqrt 2 $
Therefore, $E = \dfrac{{9 \times {{10}^9} \times {{10}^{ - 8}}}}{{{{\left( {\dfrac{a}{2}\sqrt 2 } \right)}^2}}}$
$ \Rightarrow E = \dfrac{{9 \times {{10}^9} \times {{10}^{ - 8}}}}{{{{\left( {\dfrac{{5 \times {{10}^{ - 2}}}}{2}\sqrt 2 } \right)}^2}}}$
$ \Rightarrow E = \dfrac{{9 \times 10 \times 2}}{{25 \times {{10}^{ - 4}}}}$
$ \Rightarrow E = 7.2 \times {10^4}\dfrac{N}{C}$
Hence $\overrightarrow {{E_{net}}} = 7.19 \times {10^4} \times \sqrt 2 $
$ \Rightarrow \overrightarrow {{E_{net}}} = 1.02 \times {10^5}\dfrac{N}{C}$
Hence the electric field at the center of the square is $\overrightarrow {{E_{net}}} = 1.02 \times {10^5}\dfrac{N}{C}$

Note:
The electric field in the square's center is the vector sum of the electric fields in the center caused by each of the charges separately. The algebraic total of the potentials at the center owing to each of the charges individually equals the potential at the center of the square.