Question

Four blocks and two springs are connected as shown in the figure. The system is at rest, determining the acceleration of all the loads immediately after the lower thread keeping the system in equilibrium has been cut. Assume that the threads are weightless, the mass of the pulley is negligibly small, and there is no friction at the point of suspension.

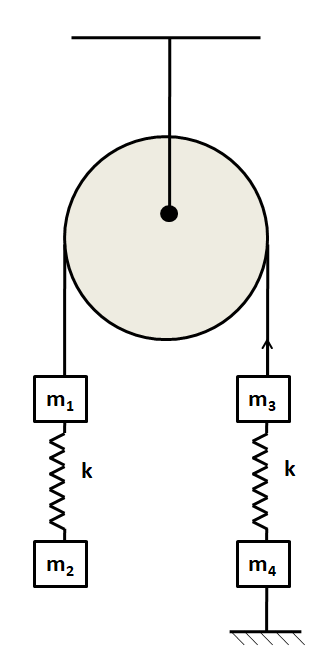
Answer 1

Hint: To solve this question, we need to find out the forces in the springs and the strings from the equilibrium of the four blocks. After the lower thread is cut, these values will remain unchanged, so applying Newton's second law of motion, we can get the accelerations of all the blocks.

Complete step by step solution:
Let the tension in the string be $T$
Also, let the forces in the left and the right springs be ${F_1}$ and ${F_2}$ respectively.
Now, if the lower thread is keeping the system in equilibrium, so the blocks at the right must be pulled up by the blocks at the right. For that, we must have
$\Rightarrow {m_1} + {m_2} > {m_3} + {m_4}$

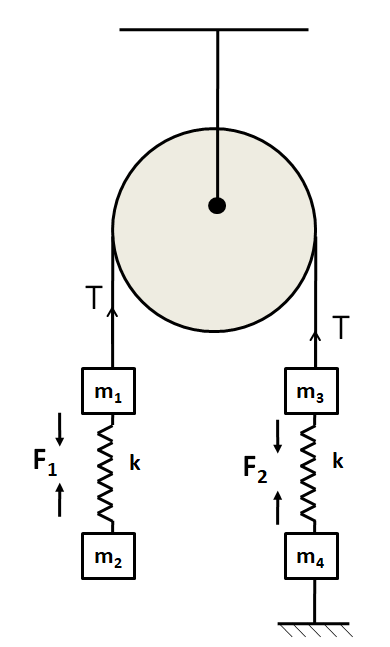
From the equilibrium of the mass ${m_2}$ we have
$\Rightarrow {F_1} = {m_2}g$ (i)
From the equilibrium of the mass ${m_1}$ we have
$\Rightarrow T = {F_1} + {m_1}g$
From (i)
$\Rightarrow T = {m_2}g + {m_1}g$
$\Rightarrow T = \left( {{m_1} + {m_2}} \right)g$ (ii)
From the equilibrium of the mass ${m_3}$
$\Rightarrow {F_2} + {m_3}g = T$
From (ii)
$\Rightarrow {F_2} + {m_3}g = \left( {{m_1} + {m_2}} \right)g$
$\Rightarrow {F_2} = \left( {{m_1} + {m_2} - {m_3}} \right)g$ (iii)
Now, when the lower thread is cut, let the acceleration of the blocks of masses${m_1}$, ${m_2}$, ${m_3}$, and ${m_4}$ be ${a_1}$ ${a_2}$, ${a_3}$, and${a_4}$respectively.
At the instant of cutting the lower thread, the extensions of the springs remain the same, and hence the forces in them will remain the same. So, ${F_1}$ and ${F_2}$ will be the same as calculated above.
Also since ${m_1} + {m_2} > {m_3} + {m_4}$, so the blocks on the left will come downward and the blocks at the right will come upwards. Therefore, the directions of the accelerations are shown as

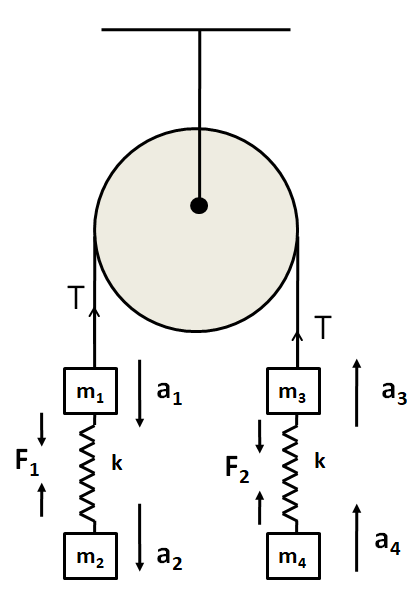
Now, we apply the Newton’s second law of motion on each of the blocks
For the block ${m_2}$
$\Rightarrow {m_2}g - {F_1} = {m_2}{a_2}$
From (i)
$\Rightarrow {m_2}g - {m_2}g = {m_2}{a_2}$
$\Rightarrow {m_2}{a_2} = 0$
Since the mass ${m_2}$ is not zero, so we have
$\Rightarrow {a_2} = 0$
For the block ${m_1}$
$\Rightarrow {m_1}g + {F_1} - T = {m_1}{a_1}$
From (i) and (ii)
$\Rightarrow {m_1}g + {m_2}g - \left( {{m_1} + {m_2}} \right)g = {m_1}{a_1}$
$\Rightarrow {m_1}{a_1} = 0$
Since the mass${m_1}$is not zero, so we have
$\Rightarrow {a_1} = 0$
For the block ${m_3}$
$\Rightarrow T - {m_3}g - {F_2} = {m_3}{a_3}$
From (ii) and (iii)
$\Rightarrow \left( {{m_1} + {m_2}} \right)g - {m_3}g - \left( {{m_1} + {m_2} - {m_3}} \right)g = {m_3}{a_3}$
$\Rightarrow \left( {{m_1} + {m_2}} \right)g - {m_3}g - \left( {{m_1} + {m_2}} \right)g + {m_3}g = {m_3}{a_3}$
On simplifying, we get
$\Rightarrow {m_3}{a_3} = 0$
Since the mass ${m_3}$ is not zero, so we have
$\Rightarrow {a_3} = 0$
For the block ${m_4}$
$\Rightarrow {F_2} - {m_4}g = {m_4}{a_4}$
From (iii)
$\Rightarrow \left( {{m_1} + {m_2} - {m_3}} \right)g - {m_4}g = {m_4}{a_4}$
$\Rightarrow \left( {{m_1} + {m_2} - {m_3} - {m_4}} \right)g = {m_4}{a_4}$
Dividing by${m_4}$we get
$\Rightarrow {a_4} = \dfrac{{\left( {{m_1} + {m_2} - {m_3} - {m_4}} \right)}}{{{m_4}}}g$
Hence, the accelerations of the blocks immediately after the lower thread is cut are
$\Rightarrow {a_1} = {a_2} = {a_3} = 0$ and ${a_4} = \dfrac{{\left( {{m_1} + {m_2} - {m_3} - {m_4}} \right)}}{{{m_4}}}g$.

Note:
There is no need to consider the tension in the lower thread and find out the value of the tension in it. Although we can find it out, it is of no use in our calculations. As we have to make all the calculations after the thread is cut, so its tension becomes zero at the instant. The tension provided by the thread before being cut is just keeping the blocks in the equilibrium.