Question

Four bells begin to toll together and then each one at intervals of 6s, 7s, 8s and 9s, respectively. The number of times they will toll together in the next 1 hour is which of the following:
(a) 7 times
(b) 8 times
(c) 6 times
(d) Never

Answer 1

Hint: First, find the LCM of 6, 7, 8, and 9 which is 504. So, the bells will toll together after every 504 seconds. Divide this b the number of seconds in an hour: 3600 seconds and find its greatest integer function to arrive at the final answer.

Complete step-by-step answer:

In this question, we are given that four bells begin to toll together and then each one at intervals of 6s, 7s, 8s and 9s, respectively.
We need to find the number of times they will toll together in the next 1 hour.
Let us first find the first time these bells will toll together.
This will be after the number of seconds equal to the LCM of 6, 7, 8, and 9.
Let us find the LCM of these numbers.

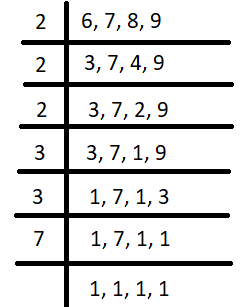
So, LCM = 2 $\times $ 2 $\times $ 2 $\times $ 3 $\times $ 3 $\times $ 7 = 504

So, the bells will toll together for the first time from the start after 504 seconds.

Or, the bells will toll together every 504 seconds.

We know that one hour consists of 3600 seconds.

So, to find the number of times these bells will toll together in an hour, we will divide 3600 by 504 and take the integer value (greatest integer function) which will be our final answer.

So, the number of times these bells will toll together in an hour = $\left[ \dfrac{3600}{504} \right]$,

Where [ ] is the greatest integer function which rounds down a real number to the nearest integer.

The number of times these bells will toll together in an hour = $\left[ \dfrac{3600}{504} \right]=\left[ 7.14 \right]=7$

So, the bells will toll together 7 times in the next one hour.

Hence, option (a) is correct.

Note: In this question, it is very important to know the method to find the LCM of two or more numbers as without it, you will not be able to solve the question. Also, it is important to know about the greatest integer function.