Question

What is the formula to find trapezoidal volume?

Answer 1

Hint: A trapezoid is a flat closed shape having 4 straight sides, with one pair of parallel sides. We commonly call trapezoid and trapezium. The parallel sides of a trapezoid are known as the bases, and its non-parallel sides are called legs. A trapezoid is a 2 dimensional figure. It cannot have a volume. In order to find the volume, we have to consider a 3 dimensional trapezoidal prism. Then, the volume of the trapezoidal prism will be the base area multiplied by length. The base area is the area of trapezium.

Complete step by step answer:
We have to write the formula for trapezoidal volume. Let us see what a trapezium is. A trapezoid is a flat closed shape having 4 straight sides, with one pair of parallel sides. We commonly call trapezoid and trapezium. The parallel sides of a trapezoid are known as the bases, and its non-parallel sides are called legs. Let us see the geometry of trapezium.
 

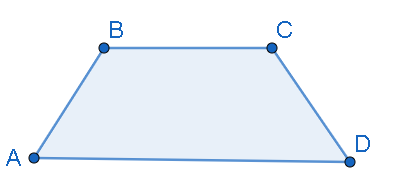
From the above figure, we can see that ABCD is a trapezium with sides BC and AD parallel and AB and CD are the legs.
We can conclude that a trapezoid is a 2 dimensional figure. It cannot have a volume. To find the volume, we will consider a 3 dimensional trapezoidal prism as shown below.

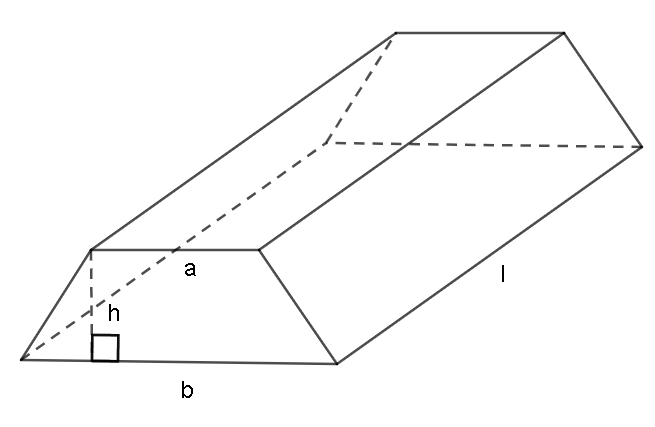
From the figure, we can see that the length of the prism is denoted by l, the height of its base is denoted as h and the parallel sides of the base are a and b.
We can write the volume of the trapezoidal prism as base area multiplied by length.
$\Rightarrow \text{Volume of trapezoidal prism}=\text{Base area}\times \text{Length}...\left( i \right)$
We know that the base of a trapezoidal prism is a trapezium. We know that area of a trapezium is given by
$\Rightarrow A=\dfrac{\left( a+b \right)}{2}h$
Let us substitute this area in (i).
$\begin{align}
  & \Rightarrow \text{Volume of trapezoidal prism}=\dfrac{a+b}{2}hl \\
 & \Rightarrow V=\dfrac{1}{2}hl\left( a+b \right) \\
\end{align}$
Therefore, there is no volume for trapezoid but the volume for trapezoidal prism is $\dfrac{1}{2}hl\left( a+b \right)$ .

Note: Students must note that for 2 dimensional shapes, only area and perimeter can be obtained. These shapes will not have volume. In the formula for volume of trapezoidal prism, students have a chance of making a mistake by writing the area as $\dfrac{a\times b}{2}h$ . In the formula for volume, we have considered the parallel sides, a and b.