Question

What is the formula for the area of a non-right angled triangle?

Answer 1

Hint: We can find area of non-right angled triangle in two ways:
1. General formula: \[\Delta Area = \dfrac{1}{2}b \times h\], where b is base length of triangle and h is height of triangle.
2. Heron’s formula: \[\Delta Area = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} \] , where \[s = \dfrac{1}{2}\left( {a + b + c} \right)\] and a,b and c are the sides of triangle. We can use any one.

Complete step by step solution:
Using general formula:
The area of ΔABC can be expressed as:
\[\Delta Area = \dfrac{1}{2}c \times h\]
Where a represents the side (base) and h represents the height drawn to that side.

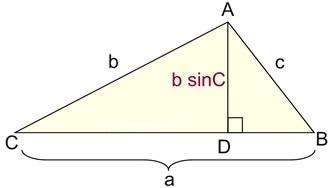
Using trigonometry, In right angled triangle CDA, we can state that
\[\sin C = \dfrac{h}{b}\] (and multiplying by b gives) \[b\sin C = h\]
The height, h of the triangle can be expressed as \[b\sin C\]
Substituting this new expression for the height, h, into the general formula for the area of a triangle gives:
\[\Delta ABC = \dfrac{1}{2}ab\sin C\]
Where a and b be two sides and C is the included angle
With this new formula, we no longer have to rely on finding the altitude (height) of a triangle in order to find its area. Now, if we know two sides and the included angle of a triangle, we can find the area of the triangle. This is a valuable new formula!
Example:
Find the area triangle whose sides are \[12\] and \[18\] and the angle between them is \[{55^ \circ }\].