Question

What is the formula for finding the perimeter of a parallelogram?

Answer 1

Hint: The perimeter is defined for a two dimensional figure as the sum of the lengths of all of its sides. For deriving the formula for the perimeter of a parallelogram, we need to first consider a parallelogram ABCD, and add all of its sides. Then by using the properties of a parallelogram, we will be able to equate the lengths of the opposite sides, and hence obtain the required formula in terms of the lengths of the adjacent sides.

Complete step by step answer:
We know that the perimeter of a two dimensional figure is equal to the sum of the lengths of all of the sides of the figure. Let us consider a parallelogram ABCD as shown in the below diagram.

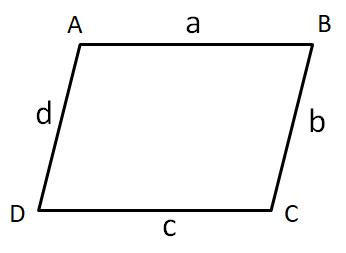
From the above figure, we can see that the lengths are
$\begin{align}
  & \Rightarrow AB=a......\left( i \right) \\
 & \Rightarrow BC=b......\left( ii \right) \\
 & \Rightarrow CD=c......\left( iii \right) \\
 & \Rightarrow DA=d......\left( iv \right) \\
\end{align}$
Since the perimeter of a two dimensional is equal to the sum of the lengths of the figure, the perimeter for the parallelogram ABCD will be given by
$\Rightarrow P=AB+BC+CD+DA$
Substituting the equations (i), (ii), (iii) and (iv) in the above equation we get
$\Rightarrow P=a+b+c+d......\left( v \right)$
Now, from the properties of the parallelogram we know that the opposite sides are parallel and equal in length. From the above figure for the parallelogram ABCD we can see that the sides AB and CD are opposite to each other. So we can write
$\Rightarrow AB=CD$
Putting the equations (i) and (iii) we can write
\[\begin{align}
  & \Rightarrow a=c \\
 & \Rightarrow c=a......\left( vi \right) \\
\end{align}\]
Also, since BC and DA are opposite, we can write
$\Rightarrow BC=DA$
Putting the equations (i) and (iii) we can write
\[\begin{align}
  & \Rightarrow b=d \\
 & \Rightarrow d=b......\left( vii \right) \\
\end{align}\]
Now, we can finally substitute the equations (vi) and (vii) into the equation (v) we get
$\begin{align}
  & \Rightarrow P=a+b+a+b \\
 & \Rightarrow P=2a+2b \\
 & \Rightarrow P=2\left( a+b \right) \\
\end{align}$
Hence, the formula for the perimeter of a parallelogram is $2\left( a+b \right)$, where a and b are the lengths of the adjacent sides.

Note: The formula for the perimeter of a parallelogram which is obtained as $2\left( a+b \right)$ is similar for the perimeter of a rectangle. This is because a rectangle is just a type of parallelogram. For the perimeter of the square and the rhombus, we can substitute $b=a$ to get $4a$ since all the sides in these are of equal length.