Question

How the formula for area of the rhombus is derived?

Answer 1

Hint:First know the structure of the rhombus and try to define it in terms of length, breadth and in angle. Know the congruent of the rhombus and its other properties. Try to convert it and fix it in a known area like rectangle, square and triangle.

Complete step by step solution:
Here, first one has to define what is meant by a rhombus; rhombus is nothing but which is in the shape of the diamond. It has four sides and all sides are equal in length. And also, it has two diagonals, in which one diagonal is always greater than the other.

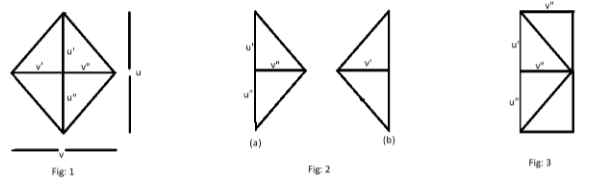
The Fig:1 shows the shape of a rhombus. The Fig: 1 has four equal sides and two unequal diagonals.

$u$ be the large diagonal and $v$ be the small diagonal. Let us divide the rhombus into two as shown in Fig 2 and the upper triangle of the Fig 2 (b) be rotated ${180^ \circ }$ anticlockwise, rotate ${180^ \circ }$upwards and fixed in the right side of the rhombus as shown in Fig: 3.

 This process should be repeated for the lower triangle also. Now the Fig: 3 resemble as a rectangle and we already know that the area of the rectangle= Length * Breadth, which also can be said as the area of the rhombus and also it will be the multiple of the larger diagonal and half of the smaller diagonal.

And hence the area of rhombus is equal to $u*\dfrac{v}{2}$, which also can be written as the Area of the rhombus$ = \dfrac{1}{2}uv$. This is the required solution.

Note: Whatever may be the shapes, we are able to find the area of any shape by comparing it to a known value. In ancient days, they found the area of the rectangle, triangle and square and to find the area of the other shapes they just compared with all these known areas.