Question

Forces of magnitude 3, P, 5, 10, Q are respectively acting along the sides AB, BC, CD, AD and the diagonal CA of a rectangle ABCD, where AB = 4m and BC = 3m. if the resultant is a single force along the other diagonal BD, then P, Q and the resultant are-
${\text{A}}{\text{. 4, 10}}\dfrac{5}{{12}},12\dfrac{{11}}{{12}}$
${\text{B}}{\text{. 5, 6}},7$
${\text{C}}{\text{. 3}}\dfrac{1}{2},8,9\dfrac{1}{2}$
${\text{D}}{\text{.}}$ None of the above

Answer 1

Hint – Draw a rough sketch of all the forces acting along the sides AB, BC, CD, AD and the diagonal CA of the rectangle ABCD, then solve the question.

Complete step-by-step answer:

Given in the question that forces of magnitude 3, P, 5, 10, Q are respectively acting along the sides AB, BC, CD, AD and the diagonal CA of a rectangle ABCD.
Also given that, AB = 4m and BC = 3m.
The figure of the rectangle ABCD showing all the forces is shown below-

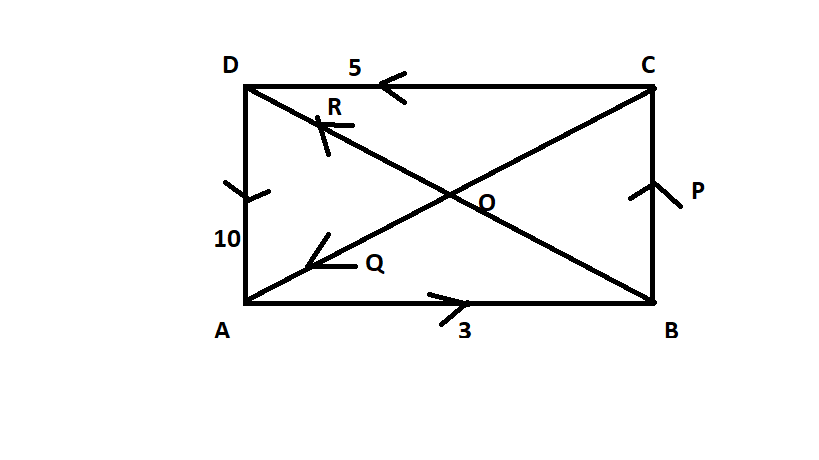
Now, if we find, $\tan \theta = \dfrac{{BC}}{{AB}} = \dfrac{3}{4}$.
Now, the forces 3, P, 5, 10 and Q Newtons have the resultant R as shown in figure.
So, we can write, $R\cos \theta + 5 - 3 = Q\cos \theta + 2 \to (1)$
And, $R\sin \theta = P + 10 - Q\sin \theta \to (2)$
Also, $QAB\sin \theta + 5.BC = 10.AB$
Or, $Q.4.\dfrac{3}{5} + 5 \times 3 = 10 \times 4\left( {\because \sin \theta = \dfrac{3}{5},\cos \theta = \dfrac{4}{5}} \right)$
Solving further, we get-
$
   \Rightarrow \dfrac{{12}}{5}Q = 40 - 15 = 25 \\
   \Rightarrow Q = \dfrac{{125}}{{12}} \\
 $
Then, find R from equation (1) and P from equation (2).
$
  \dfrac{{4R}}{5} = \dfrac{{125}}{{12}} \times \dfrac{4}{5} + 2 \\
   \Rightarrow 4R = \dfrac{{125}}{3} + 10 = \dfrac{{155}}{3} \\
   \Rightarrow R = \dfrac{{155}}{{12}} \\
 $
And $
  \dfrac{{155}}{{12}} \times \dfrac{3}{5} = P + 10 - \dfrac{{125}}{{12}} \times \dfrac{3}{5} \\
   \Rightarrow \dfrac{{155}}{4} = 5P + 50 - \dfrac{{125}}{4} \\
   \Rightarrow 5P = \dfrac{{155}}{4} + \dfrac{{125}}{4} - 50 \\
   \Rightarrow 5P = \dfrac{{280}}{4} - 50 = 70 - 50 = 20 \\
   \Rightarrow P = 4. \\
 $
Hence, the forces along the diagonal BD is $R = \dfrac{{155}}{{12}} = 12\dfrac{{11}}{{12}}$ , the value of forces P and Q are $P = 4$ and $Q = 10\dfrac{5}{{12}}$ , respectively.
Hence, the correct option is ${\text{A}}{\text{. 4, 10}}\dfrac{5}{{12}},12\dfrac{{11}}{{12}}$.

Note – Whenever such types of questions appear, then always note down the things given in the question first. Then draw the figure using the information given in the question. And then applying basic mathematics from the equations and solving them to get the result.