Question

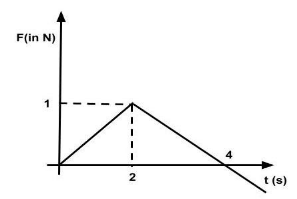
Force acting on a body varies with time as shown below. If the initial momentum of the body is \[\mathop P\limits^ \to \] then the time taken by the body to retain its momentum \[\mathop P\limits^ \to \]​ again is?
A. $8s$
B. $\left( {4 + \sqrt[2]{2}} \right)s$
C. $6s$
D. Can never be obtained.

Answer 1

Hint: In physics, a force is any interaction that, while unopposed, causes an object to change its velocity. As a result of a force, an object with mass can change its velocity, or accelerate. Force is intuitively described as a push or a pull. Because it has both magnitude and direction, a force is a vector quantity.

Complete step by step answer:
For $t = 0$ to $t = 2$ , Force equation can be written in the standard form;
$y = mx + c$
${\mathop F _1}\left( t \right) = \dfrac{t}{2}$
When a force acts on a mass, Newton's Second Law of Motion states that acceleration (gaining speed) occurs (object). According to Newton's Second Law, the larger the mass of the item being propelled, the more force is required to accelerate the object.
Let, $m$ be the mass of body from Newton’s second law of motion
$\mathop a\limits^ \to (t) = \dfrac{1}{m} \times \dfrac{t}{2}$
Acceleration,
$\mathop a\limits^ \to \equiv \dfrac{{d\mathop v\limits^ \to }}{{dt}} \\
\Rightarrow \mathop v\limits^ \to (t) = \dfrac{1}{m}\int {\dfrac{t}{2}} dt \\
\Rightarrow \dfrac{{\overrightarrow p }}{m} = c \\
\mathop v\limits^ \to (t) = \dfrac{1}{m}\left( {\dfrac{{{t^2}}}{4} + \mathop p\limits^ \to } \right)\,\,......(1) \\ $
Velocity at $t = 2$ is found as
$\mathop v\limits^ \to (2) = \dfrac{1}{m}\left( {1 + \mathop p\limits^ \to } \right)\,\,.........(2)$
Velocity at $t = 2$ and thereafter becomes
$\mathop F\limits^ \to (t) = - \dfrac{1}{2}t + 2 \\
\Rightarrow \mathop a\limits^ \to (t) = - \dfrac{1}{m}\left( {\dfrac{t}{2} - 2} \right) \\
\Rightarrow {\mathop v_2}(t) = - \dfrac{1}{m}\int {\left( {\dfrac{t}{2} - 2} \right)} \,dt \\
\Rightarrow {\mathop v_2}(t) = - \dfrac{1}{m}\left( {\dfrac{{{t^2}}}{4} - 2t + {C_1}} \right) \\ $
Where, ${C_1}$ is constant of integration
Using (2) to find out ${C_1}$
${\mathop v _2}(2) = - \dfrac{1}{m}\left( {\dfrac{{{t^2}}}{4} - 2t + 2 - \mathop p\limits^ \to } \right)\,\,......(3)$
Imposing the given condition we will solve for $t$ :
$- \mathop p\limits^ \to = \dfrac{{{t^2}}}{4} - 2t + 2 - \mathop p\limits^ \to \\
\Rightarrow {t^2} - 8t + 8 = 0 \\ $
Solution of the quadratic gives us
$t = \dfrac{{8 \pm \sqrt {64 - 4 \times 1 \times 8} }}{2} \\
\therefore t = 4 \pm \sqrt[2]{2} \\ $
For the original query, only the $ - ve$ sign will suffice. We have two answers for the magnitude of momentum, as shown above.

Note: Most people's instinctive notion of momentum is that a large, fast-moving item has more momentum than a smaller, slower thing. The product of a system's mass multiplied by its velocity is defined as linear momentum. Linear momentum is written as \[p{\text{ }} = {\text{ }}mv\] in symbols. The mass and velocity of an object are both directly related to its momentum. As a result, the larger an object's mass or velocity, the higher its momentum.