Question

For what values of $y$ are points $P\left( 1,4 \right),Q\left( 3,y \right)$ and $R\left( -3,16 \right)$ are collinear?

Answer 1

Hint: This question is related to topic coordinate geometry. In this question we have to find the value of $y$ for which these points are collinear. For this we will use the formula of area of triangle of coordinate geometry then we will put this value of area of triangle equal to $0$ and this will give us an equation of one variable and from that we will find the value of $y$ .

Complete step by step answer:
This question is related to chapter coordinate geometry.
In this question we have to find $y$ for which our given points will be collinear.
So to understand this question properly we will first understand the meaning of collinear points.
Collinear points
Collinear points are the points which lie on the same line.
Let us understand this with an example

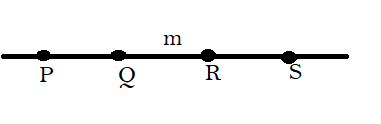
In this diagram there is a line named as $m$ and $P,Q,R$ $\And $ $S$ are points on the line.
As we can see all the points are on the same line so they will be called collinear points.

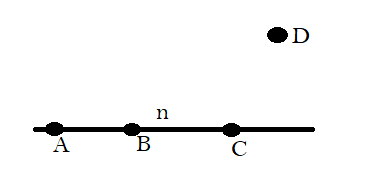
In this diagram there is a line named as $n$ and $A,B,C\And D$ are the points.
$A,B\And C$ Points are on the line $n$ but point $D$ is not on the line.
So we cannot say that that $A,B,C\And D$are collinear points.
So $A,B,C\And D$ points are called non collinear points.
From the diagrams we can observe that collinear points cannot make a triangle
We will use this point further in this question.

Now we will proceed to our question.
In the question our given points are $P\left( 1,4 \right),Q\left( 3,y \right)$ and $R\left( -3,16 \right)$.
If these points are collinear then they cannot form triangle so area of triangle formed by them have $0$ area, means area$\vartriangle PQR=0$
Formula for area of triangle with coordinates $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$
Area of triangle $=\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]$
So according to our given question,
$\begin{align}
  & {{x}_{1}}=1 \\
 & {{y}_{1}}=4 \\
 & {{x}_{2}}=3 \\
 & {{y}_{2}}=y \\
 & {{x}_{3}}=-3 \\
 & {{y}_{3}}=16 \\
\end{align}$
Now we will substitute these values in formula for area of triangle with coordinates $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$
Area of triangle $=\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]$
Area of triangle $=\dfrac{1}{2}\left[ 1\left( y-16 \right)+3\left( 16-4 \right)+\left( -3 \right)\left( 4-y \right) \right]$
As we know area of triangle $=0$
$0=\dfrac{1}{2}\left[ 1\left( y-16 \right)+3\left( 16-4 \right)+\left( -3 \right)\left( 4-y \right) \right]$
We can also write it as
$\dfrac{1}{2}\left[ 1\left( y-16 \right)+3\left( 16-4 \right)+\left( -3 \right)\left( 4-y \right) \right]=0$
Now we will solve this equation find value of $y$
$\begin{align}
  & \dfrac{1}{2}\left[ y-16+3\times 12-12+3y \right] \\
 & \Rightarrow \dfrac{1}{2}\left[ 4y-16+36-12 \right] \\
 & \Rightarrow \dfrac{1}{2}\left[ 4y+8 \right] \\
\end{align}$
Now we will substitute this simpler equation equal to $0$
$\begin{align}
  & \dfrac{1}{2}\left[ 4y+8 \right]=0 \\
 & \Rightarrow 4y+8=0 \\
 & \Rightarrow 4y=-8 \\
 & \Rightarrow y=-2 \\
\end{align}$
$\therefore y=-2$ is our required answer which means if $y=-2$ then our given points will be collinear.

Note:
Along with the area of the triangle there are other important formulas in coordinate geometry. Like Distance Formula which is used to find the distance between any two points, Midpoint Formula which is used to find the midpoint of the line formed by joining any two points and Section Formula which is used to find the ratio in which the third point will cut the line formed by joining any two points.