Question

For what value of k, \[\left( 4-k \right){{x}^{2}}+2\left( k+2 \right)x+\left( 8k+1 \right)\] is a perfect square.
\[\left( a \right)k=3\]
\[\left( b \right)k=0\]
(c) does not exist
(d) Both (a) and (b)

Answer 1

Hint: To solve this question, observe the quadratic equation given as \[a{{x}^{2}}+bx+c=0\] where this equation has 2 equal roots, then its discriminant \[D={{b}^{2}}-4ac\] becomes equal to zero. We will use this concept to solve this question. When the value of the given equation is a perfect square, the roots are equal, so we get, \[D={{b}^{2}}-4ac=0.\]

Complete step-by-step solution
We are given the value \[\left( 4-k \right){{x}^{2}}+2\left( k+2 \right)x+\left( 8k+1 \right)\] is a perfect square. This above given is a quadratic equation. A quadratic equation is of order 2. It has two roots, therefore the above-given equation being quadratic has 2 roots.
\[\Rightarrow \left( 4-k \right){{x}^{2}}+2\left( k+2 \right)x+\left( 8k+1 \right)\] has 2 roots.
We are given that this equation is a perfect square. So, both the roots are equal as then only they can form \[{{a}^{'}}\times {{a}^{'}}={{\left( {{a}^{'}} \right)}^{2}}\] where a is the root (assumed). When our equation is given of the form, \[a{{x}^{2}}+bx+c=0\] and the roots are equal.
\[\Rightarrow \Delta =D={{b}^{2}}-4ac=0\]
That is, their discriminant is equal to zero.
Comparing our equation from \[a{{x}^{2}}+bx+c=0,\] we get,
\[a=\left( 4-k \right)\]
\[b=2\left( k+2 \right)\]
\[c=8k+1\]
Using \[D=\Delta ={{b}^{2}}-4ac\] in our equation, we get, \[{{b}^{2}}-4ac=0.\]
\[\Rightarrow {{\left( 2\left( k+2 \right) \right)}^{2}}-4\times \left( 4-k \right)\left( 8k+1 \right)=0\]
Opening the square using the formula \[{{\left( x+y \right)}^{2}}={{x}^{2}}+{{y}^{2}}+2xy,\] we get,
\[\Rightarrow {{2}^{2}}\left( {{k}^{2}}+4+4k \right)-4\left( 4-k \right)\left( 8k+1 \right)=0\]
Solving further, we have,
\[\Rightarrow 4\left[ {{k}^{2}}+4+4k-\left[ 8k\times 4+4-8{{k}^{2}}-k \right] \right]=0\]
\[\Rightarrow {{k}^{2}}+4+4k-32k-4+8{{k}^{2}}+k=0\]
\[\Rightarrow 9{{k}^{2}}-27k=0\]
Cancelling 9 by taking the common
\[\Rightarrow 9\left( {{k}^{2}}-3k \right)=0\]
As, \[9\ne 0,\]
\[\Rightarrow {{k}^{2}}-3k=0\]
\[\Rightarrow k\left( k-3 \right)=0\]
\[\Rightarrow k=0;k=3\]
Therefore, for the term \[\left( 4-k \right){{x}^{2}}+2\left( k+2 \right)x+\left( 8k+1 \right)\] to be a perfect square, k = 0 or k = 3.
Hence, option (d) is the right answer.

Note: The case when the roots are equal is represented graphically as

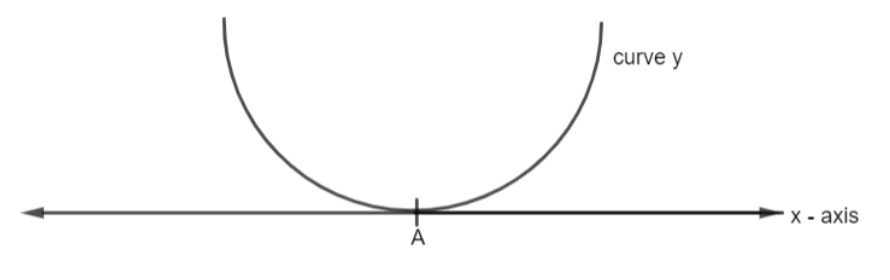
At point A, \[D={{b}^{2}}-4ac=0,\] that is discriminant is zero and hence the roots are equal. For single roots, the curve cuts the x-axis once. For example, we have a single root at B.