For triangle ABC, $A\left( 1,3 \right),C\left( \dfrac{-2}{5},\dfrac{-2}{5} \right)$ and angle bisector of angle ABC is $x+y=2$? Find: -
(a) Equation of BC
(b) Coordinates of B
(c) Equation of AB
Answer
Verified519k+ views
Hint: Assume the coordinates of B as (x, y), slope of line BC as ${{m}_{1}}$ and the slope of line AB as ${{m}_{2}}$. Find the angle between the lines BC and $x+y=2$ using the relation ${{\tan }^{-1}}\left| \dfrac{m-{{m}_{1}}}{1+m{{m}_{1}}} \right|$ where m is the slope of the line $x+y=2$. Similarly, find the angle between the lines AB and $x+y=2$ using the relation ${{\tan }^{-1}}\left| \dfrac{m-{{m}_{2}}}{1+m{{m}_{2}}} \right|$. Equate the two angles and find the relation between ${{m}_{1}}$ and ${{m}_{2}}$. Use the formula slope = $\dfrac{\Delta y}{\Delta x}$ and find the values of ${{m}_{1}}$ and ${{m}_{2}}$ in terms of x and y. Substitute them in the obtained relation of the slopes and solve the equation to get the values of x and y. Finally, find the equation of the lines using the slope form given as $\left( y-{{y}_{1}} \right)={{m}_{1}}\left( x-{{x}_{1}} \right)$ and $\left( y-{{y}_{2}} \right)={{m}_{2}}\left( x-{{x}_{2}} \right)$. Here $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the coordinates of C and A respectively.
Complete step by step answer:
Here we have been provided with a triangle ABC with the coordinates of A and C. Also, the equation of the angle bisector of angle B is given. We have been asked to find the equation of sides AB and BC. Also we have to determine the coordinates of point B. First let us draw a diagram of the given situation.
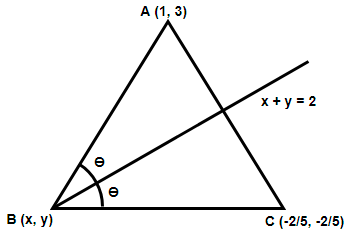
In the above diagram we have assumed the slope of line BC as ${{m}_{1}}$ and the slope of line AB as ${{m}_{2}}$. We need to determine the values of ${{m}_{1}}$ and ${{m}_{2}}$. Assuming the slope of line $x+y=2$ as m, we have,
$\begin{align}
& \Rightarrow x+y=2 \\
& \Rightarrow y=-x+2 \\
\end{align}$
Comparing it with the slope intercept form of a line given as $y=mx+c$ we get the value of m = -1. Therefore the slope of the line $x+y=2$ is -1. We know that the angle between the two lines having slopes p and q is given as ${{\tan }^{-1}}\left| \dfrac{p-q}{1+pq} \right|$, so the angle between the lines BC and $x+y=2$ will be ${{\tan }^{-1}}\left| \dfrac{1-{{m}_{1}}}{1+{{m}_{1}}} \right|$ and similarly the angle between the lines AB and $x+y=2$ will be ${{\tan }^{-1}}\left| \dfrac{1-{{m}_{2}}}{1+{{m}_{2}}} \right|$. As the two angles are equal because $x+y=2$ is the angle bisector of angle B, we get,
$\Rightarrow {{\tan }^{-1}}\left| \dfrac{1-{{m}_{1}}}{1+{{m}_{1}}} \right|={{\tan }^{-1}}\left| \dfrac{1-{{m}_{2}}}{1+{{m}_{2}}} \right|$
Removing the inverse tangent function and the modulus function from both the sides we get,
$\Rightarrow \left( \dfrac{1-{{m}_{1}}}{1+{{m}_{1}}} \right)=\pm \left( \dfrac{1-{{m}_{2}}}{1+{{m}_{2}}} \right)$
(1) Considering the positive sign we get,
$\begin{align}
& \Rightarrow \left( \dfrac{1-{{m}_{1}}}{1+{{m}_{1}}} \right)=\left( \dfrac{1-{{m}_{2}}}{1+{{m}_{2}}} \right) \\
& \Rightarrow 1+{{m}_{2}}-{{m}_{1}}-{{m}_{1}}{{m}_{2}}=1-{{m}_{2}}+{{m}_{1}}-{{m}_{1}}{{m}_{2}} \\
& \Rightarrow {{m}_{1}}={{m}_{2}} \\
\end{align}$
(2) Considering the negative sign we get,
$\begin{align}
& \Rightarrow \left( \dfrac{1-{{m}_{1}}}{1+{{m}_{1}}} \right)=-\left( \dfrac{1-{{m}_{2}}}{1+{{m}_{2}}} \right) \\
& \Rightarrow 1+{{m}_{2}}-{{m}_{1}}-{{m}_{1}}{{m}_{2}}=-1+{{m}_{2}}-{{m}_{1}}+{{m}_{1}}{{m}_{2}} \\
& \Rightarrow {{m}_{1}}{{m}_{2}}=1 \\
\end{align}$
Now, if the slopes of the line AB and BC will be equal then either they will be parallel or they will overlap depending of the value of constants in their equations. In both the cases then will not form a triangle because they need to intersect at a point to form a triangle, so ${{m}_{1}}={{m}_{2}}$ is the incorrect relation. We have to consider the relation ${{m}_{1}}{{m}_{2}}=1$.
We know that slope of a line is also given as slope = $\dfrac{\Delta y}{\Delta x}$, so slope of the lines BC will be given as:
$\begin{align}
& \Rightarrow {{m}_{1}}=\dfrac{y-\left( -\dfrac{2}{5} \right)}{x-\left( -\dfrac{2}{5} \right)} \\
& \Rightarrow {{m}_{1}}=\dfrac{5y+2}{5x+2} \\
\end{align}$
Similarly, the slope of AB will be given as:
$\Rightarrow {{m}_{2}}=\dfrac{y-3}{x-1}$
Substituting these values in the relation ${{m}_{1}}{{m}_{2}}=1$ we get,
\[\begin{align}
& \Rightarrow \left( \dfrac{5y+2}{5x+2} \right)\left( \dfrac{y-3}{x-1} \right)=1 \\
& \Rightarrow \left( 5y+2 \right)\left( y-3 \right)=\left( 5x+2 \right)\left( x-1 \right) \\
& \Rightarrow 5{{y}^{2}}-6-13y=5{{x}^{2}}-2-3x \\
\end{align}\]
Since point B lies on the line $x+y=2$ so its coordinates must satisfy this line. Substituting the value of x in term of y in the above relation we get,
\[\begin{align}
& \Rightarrow 5{{y}^{2}}-6-13y=5{{\left( 2-y \right)}^{2}}-2-3\left( 2-y \right) \\
& \Rightarrow 5{{y}^{2}}-6-13y=20+5{{y}^{2}}-20y-2-6+3y \\
& \Rightarrow y=\dfrac{9}{2} \\
\end{align}\]
Substituting the value of y in the equation $x+y=2$ we get,
\[\begin{align}
& \Rightarrow x=2-\dfrac{9}{2} \\
& \Rightarrow x=-\dfrac{5}{2} \\
\end{align}\]
(b) Therefore, the coordinates of point B is $\left( -\dfrac{5}{2},\dfrac{9}{2} \right)$.
Therefore the slopes of the lines BC and AB will be given as:
$\Rightarrow {{m}_{1}}=\dfrac{5\left( \dfrac{9}{2} \right)+2}{5\left( -\dfrac{25}{2} \right)+2}=\left( -\dfrac{7}{3} \right)$ and ${{m}_{2}}=\dfrac{1}{{{m}_{1}}}=\left( -\dfrac{3}{7} \right)$.
(a) Now, we know that the equation of a line passing through a point (a, b) and having slope k in slope form is given as$\left( y-b \right)=k\left( x-a \right)$. So considering that the line BC passes through the point $C\left( \dfrac{-2}{5},\dfrac{-2}{5} \right)$ and has slope ${{m}_{1}}=\left( -\dfrac{7}{3} \right)$ we can write its equation as:
\[\begin{align}
& \Rightarrow \left( y-\left( -\dfrac{2}{5} \right) \right)=\left( -\dfrac{7}{3} \right)\left( x-\left( -\dfrac{2}{5} \right) \right) \\
& \therefore 7x+3y+4=0 \\
\end{align}\]
(c) Similarly, considering that the line AB passes through the point $A\left( 1,3 \right)$ and has slope ${{m}_{2}}=\left( -\dfrac{3}{7} \right)$ we can write its equation as:
\[\begin{align}
& \Rightarrow \left( y-3 \right)=\left( -\dfrac{3}{7} \right)\left( x-1 \right) \\
& \therefore 7y+3x-24=0 \\
\end{align}\]
Note: Always draw the figure for better understanding. Remember the formulas of angle between the two lines, general equations of the slope intercept and slope form of a line. Now, if you are asked to determine the area of the triangle then you can easily apply the formula given in coordinate geometry. Always check if a given condition is satisfied or not by understanding it geometrically and reject the relation which does not satisfy.
Complete step by step answer:
Here we have been provided with a triangle ABC with the coordinates of A and C. Also, the equation of the angle bisector of angle B is given. We have been asked to find the equation of sides AB and BC. Also we have to determine the coordinates of point B. First let us draw a diagram of the given situation.
In the above diagram we have assumed the slope of line BC as ${{m}_{1}}$ and the slope of line AB as ${{m}_{2}}$. We need to determine the values of ${{m}_{1}}$ and ${{m}_{2}}$. Assuming the slope of line $x+y=2$ as m, we have,
$\begin{align}
& \Rightarrow x+y=2 \\
& \Rightarrow y=-x+2 \\
\end{align}$
Comparing it with the slope intercept form of a line given as $y=mx+c$ we get the value of m = -1. Therefore the slope of the line $x+y=2$ is -1. We know that the angle between the two lines having slopes p and q is given as ${{\tan }^{-1}}\left| \dfrac{p-q}{1+pq} \right|$, so the angle between the lines BC and $x+y=2$ will be ${{\tan }^{-1}}\left| \dfrac{1-{{m}_{1}}}{1+{{m}_{1}}} \right|$ and similarly the angle between the lines AB and $x+y=2$ will be ${{\tan }^{-1}}\left| \dfrac{1-{{m}_{2}}}{1+{{m}_{2}}} \right|$. As the two angles are equal because $x+y=2$ is the angle bisector of angle B, we get,
$\Rightarrow {{\tan }^{-1}}\left| \dfrac{1-{{m}_{1}}}{1+{{m}_{1}}} \right|={{\tan }^{-1}}\left| \dfrac{1-{{m}_{2}}}{1+{{m}_{2}}} \right|$
Removing the inverse tangent function and the modulus function from both the sides we get,
$\Rightarrow \left( \dfrac{1-{{m}_{1}}}{1+{{m}_{1}}} \right)=\pm \left( \dfrac{1-{{m}_{2}}}{1+{{m}_{2}}} \right)$
(1) Considering the positive sign we get,
$\begin{align}
& \Rightarrow \left( \dfrac{1-{{m}_{1}}}{1+{{m}_{1}}} \right)=\left( \dfrac{1-{{m}_{2}}}{1+{{m}_{2}}} \right) \\
& \Rightarrow 1+{{m}_{2}}-{{m}_{1}}-{{m}_{1}}{{m}_{2}}=1-{{m}_{2}}+{{m}_{1}}-{{m}_{1}}{{m}_{2}} \\
& \Rightarrow {{m}_{1}}={{m}_{2}} \\
\end{align}$
(2) Considering the negative sign we get,
$\begin{align}
& \Rightarrow \left( \dfrac{1-{{m}_{1}}}{1+{{m}_{1}}} \right)=-\left( \dfrac{1-{{m}_{2}}}{1+{{m}_{2}}} \right) \\
& \Rightarrow 1+{{m}_{2}}-{{m}_{1}}-{{m}_{1}}{{m}_{2}}=-1+{{m}_{2}}-{{m}_{1}}+{{m}_{1}}{{m}_{2}} \\
& \Rightarrow {{m}_{1}}{{m}_{2}}=1 \\
\end{align}$
Now, if the slopes of the line AB and BC will be equal then either they will be parallel or they will overlap depending of the value of constants in their equations. In both the cases then will not form a triangle because they need to intersect at a point to form a triangle, so ${{m}_{1}}={{m}_{2}}$ is the incorrect relation. We have to consider the relation ${{m}_{1}}{{m}_{2}}=1$.
We know that slope of a line is also given as slope = $\dfrac{\Delta y}{\Delta x}$, so slope of the lines BC will be given as:
$\begin{align}
& \Rightarrow {{m}_{1}}=\dfrac{y-\left( -\dfrac{2}{5} \right)}{x-\left( -\dfrac{2}{5} \right)} \\
& \Rightarrow {{m}_{1}}=\dfrac{5y+2}{5x+2} \\
\end{align}$
Similarly, the slope of AB will be given as:
$\Rightarrow {{m}_{2}}=\dfrac{y-3}{x-1}$
Substituting these values in the relation ${{m}_{1}}{{m}_{2}}=1$ we get,
\[\begin{align}
& \Rightarrow \left( \dfrac{5y+2}{5x+2} \right)\left( \dfrac{y-3}{x-1} \right)=1 \\
& \Rightarrow \left( 5y+2 \right)\left( y-3 \right)=\left( 5x+2 \right)\left( x-1 \right) \\
& \Rightarrow 5{{y}^{2}}-6-13y=5{{x}^{2}}-2-3x \\
\end{align}\]
Since point B lies on the line $x+y=2$ so its coordinates must satisfy this line. Substituting the value of x in term of y in the above relation we get,
\[\begin{align}
& \Rightarrow 5{{y}^{2}}-6-13y=5{{\left( 2-y \right)}^{2}}-2-3\left( 2-y \right) \\
& \Rightarrow 5{{y}^{2}}-6-13y=20+5{{y}^{2}}-20y-2-6+3y \\
& \Rightarrow y=\dfrac{9}{2} \\
\end{align}\]
Substituting the value of y in the equation $x+y=2$ we get,
\[\begin{align}
& \Rightarrow x=2-\dfrac{9}{2} \\
& \Rightarrow x=-\dfrac{5}{2} \\
\end{align}\]
(b) Therefore, the coordinates of point B is $\left( -\dfrac{5}{2},\dfrac{9}{2} \right)$.
Therefore the slopes of the lines BC and AB will be given as:
$\Rightarrow {{m}_{1}}=\dfrac{5\left( \dfrac{9}{2} \right)+2}{5\left( -\dfrac{25}{2} \right)+2}=\left( -\dfrac{7}{3} \right)$ and ${{m}_{2}}=\dfrac{1}{{{m}_{1}}}=\left( -\dfrac{3}{7} \right)$.
(a) Now, we know that the equation of a line passing through a point (a, b) and having slope k in slope form is given as$\left( y-b \right)=k\left( x-a \right)$. So considering that the line BC passes through the point $C\left( \dfrac{-2}{5},\dfrac{-2}{5} \right)$ and has slope ${{m}_{1}}=\left( -\dfrac{7}{3} \right)$ we can write its equation as:
\[\begin{align}
& \Rightarrow \left( y-\left( -\dfrac{2}{5} \right) \right)=\left( -\dfrac{7}{3} \right)\left( x-\left( -\dfrac{2}{5} \right) \right) \\
& \therefore 7x+3y+4=0 \\
\end{align}\]
(c) Similarly, considering that the line AB passes through the point $A\left( 1,3 \right)$ and has slope ${{m}_{2}}=\left( -\dfrac{3}{7} \right)$ we can write its equation as:
\[\begin{align}
& \Rightarrow \left( y-3 \right)=\left( -\dfrac{3}{7} \right)\left( x-1 \right) \\
& \therefore 7y+3x-24=0 \\
\end{align}\]
Note: Always draw the figure for better understanding. Remember the formulas of angle between the two lines, general equations of the slope intercept and slope form of a line. Now, if you are asked to determine the area of the triangle then you can easily apply the formula given in coordinate geometry. Always check if a given condition is satisfied or not by understanding it geometrically and reject the relation which does not satisfy.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success
Master Class 11 English: Engaging Questions & Answers for Success
Master Class 11 Social Science: Engaging Questions & Answers for Success
Master Class 11 Biology: Engaging Questions & Answers for Success
Class 11 Question and Answer - Your Ultimate Solutions Guide
Master Class 11 Business Studies: Engaging Questions & Answers for Success
Trending doubts
10 examples of friction in our daily life
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE
Difference Between Prokaryotic Cells and Eukaryotic Cells
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE
Explain zero factorial class 11 maths CBSE
What is a periderm How does periderm formation take class 11 biology CBSE