Question

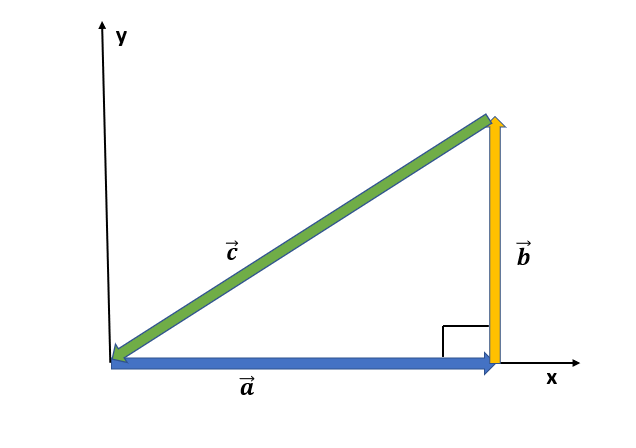
For the vector in fig., with $a = 4$, $b = 3$ and $c = 5$, what are (a) the magnitude and (b) the direction of $\vec{a} \times \vec{c}$ (c) the magnitude and (d) the direction of $\vec{a} \times \vec{b}$, and the magnitude and (f) the direction of $\vec{b} \times \vec{c}$(the z-axis is not shown)

Answer 1

Hint: Cross product is a binary procedure on two vectors in $3-D$ space. Given two linearly independent vectors, a and b, the cross product of a and b is a perpendicular vector to both a and b. If two vectors have the identical direction or have the opposite direction from one another or have zero length, then their vector product is zero.

Complete step-by-step solution:
Given: $|\vec{a}| = 4$, $|\vec{b}| = 3$, $|\vec{c}| = 5$

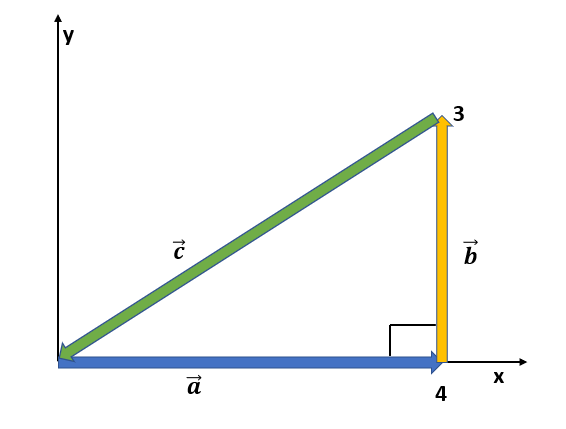
From figure, $\vec{a} = 4 \hat{i}$, $\vec{b} = 3 \hat{j}$ and $\vec{c} = 4 \hat{i} + 3 \hat{j}$
a) First, we find the magnitude of $\vec{a} \times \vec{c}$,
$\vec{a} \times \vec{c} = 4 \hat{i} \times (4 \hat{i} + 3 \hat{j}) $
$\vec{a} \times \vec{c} = 16 (\hat{i} \times \hat{i}) + 12 (\hat{i} \times \hat{j}) $
$\vec{a} \times \vec{c} = 12 \hat{k} $
b) The direction of $\vec{a} \times \vec{c}$ is $\hat{k}$.
c) Now, we find the magnitude $\vec{a} \times \vec{b}$,
$\vec{a} \times \vec{b} = 4 \hat{i} \times 3 \hat{j} $
$\vec{a} \times \vec{b} = 12 (\hat{i} \times \hat{j}) $
$\vec{a} \times \vec{b} = 12 \hat{k} $
d) The direction of $\vec{a} \times \vec{b}$ is $\hat{k}$.
e) First, we find the magnitude of $\vec{b} \times \vec{c}$
$\vec{b} \times \vec{c} = 3 \hat{j} \times (4 \hat{i} + 3 \hat{j}) $
$\vec{b} \times \vec{c} = 12 (\hat{j} \times \hat{i}) + 9 (\hat{j} \times \hat{j}) $
$\vec{b} \times \vec{c} = -12 \hat{k} $
f) The direction of $\vec{b} \times \vec{c}$ is $\hat{-k}$.

Note:More commonly, the magnitude of the cross product is equal to the area of a parallelogram with vectors for sides; in particular, the magnitude of the product of two perpendicular vectors is the product of their lengths. The right-hand thumb rule is utilized in which we turn up the fingers of the right hand about a line perpendicular to the vectors planes a and b and fold the fingers in the way from a to b, then the extended thumb points in the way of c.