Question

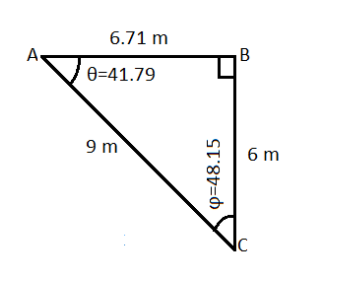
For the right triangle shown in figure above, what are
(a) the length of the unknown side,
(b) the tangent of $ \theta $ , and
(c) the sine of $ \phi $ ?

Answer 1

Hint: Pythagoras theorem: Pythagoras theorem is used in the right angle triangle. It is used to find the one known side if the two sides are given. It states that “the sum of the square of height and base are always equal to the square of hypotenuse. Which triangle fills this criteria is also called a right angle triangle.
As we know that
 $ {h^2} = {b^2} + {l^2} $
Here,
h=hypotenuse
b=base
l=height

Complete step-by-step answer:
Given,
Length of hypotenuse $ = 9m $
Length of height $ = 6m $
Using the Pythagoras theorem is given by
 $ \Rightarrow {h^2} = {b^2} + {l^2} $
So we find the base then,
 $ \Rightarrow b = \sqrt {{h^2} - {l^2}} $
Put the value in equation
 $ \Rightarrow b = \sqrt {{9^2} - {6^2}} $
 $ \Rightarrow b = \sqrt {81 - 36} $
 $ \Rightarrow b = \sqrt {45} $
Factorize the 45
 $ \Rightarrow 45 = 3 \times 3 \times 5 $
Put above
 $ \Rightarrow b = \sqrt {3 \times 3 \times 5} $
Make the set and take out from radical
 $ \Rightarrow b = 3\sqrt 5 m $
 $ \Rightarrow b = 6.71m $
Hence the length of base is $ 6.71m $

(b) Now find the tangent of $ \theta $
Tangent is the ratio of side opposite the angle and side adjacent to angle
Side opposite the angle $ = 6m $
Side adjacent the angle $ = 6.71m $
Put the value
 $ \Rightarrow \tan \theta = \dfrac{6}{{6.71}} $
 $ \Rightarrow \tan \theta = 0.894 $
(b) Now find the sine of $ \phi $
Sine is the ratio of side opposite the angle and hypotenuse of triangle
Side opposite the angle $ = 6.71m $
Hypotenuse of the triangle $ = 9m $
Put the value
 $ \Rightarrow \sin \phi = \dfrac{{6.71}}{9} $
 $ \Rightarrow \sin \phi = 0.745 $

Note: Trigonometry is the branch of mathematics which deals with the relationship between side lengths and angle of triangles. There are six trigonometric ratios they are- sine, cosine, tangent, cosecant, secant, and cotangent. And their abbreviations are sin, cos, tan, cot, cosec, and sec. Right Angle Triangle Properties- One angle is always 90° or right angle. The side opposite angle 90° is the hypotenuse. The hypotenuse is always the longest side. The sum of the other two interior angles is equal to 90°. The other two sides adjacent to the right angle are called base and perpendicular.