Question

For the parabola ${{y}^{2}}+6y-2x+5=0$
(I) The vertex is (-2, -3)
(II) The directrix is y+3=0
Which of the following is correct?
(a) Both I and II are true
(b) I is true, II is false
(c) I is false, II is true
(d) Both I and II are false

Answer 1

Hint: First, before proceeding for this, we must draw the parabola to get the idea whether the given statements are true or not. Then, by using the completing the square method and adding and subtracting ${{\left( -3 \right)}^{2}}$, we get the general equation of the parabola is as ${{\left( y-k \right)}^{2}}=4a\left( x-h \right)$ where (h, k) is the vertex. Then, we also know that the equation of the directrix of parabola is given by $x-h+a=0$ which gives the conclusion for both statements.

Complete step-by-step answer:
In this question, we are supposed to find that the given statements as the vertex is (-2, -3) and the directrix is y+3=0 for the parabola as ${{y}^{2}}+6y-2x+5=0$.
So, before proceeding for this, we must draw the parabola to get the idea whether the given statements are true or not as:

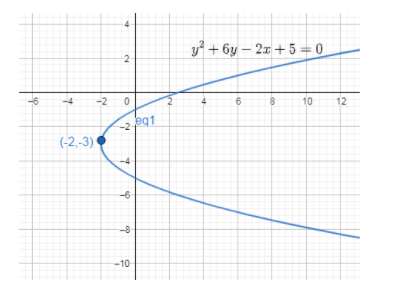
Then, from the figure we can clearly see that the vertex is (-2, -3) but still we go by conventional method.
So, by using the completing the square method and adding and subtracting ${{\left( -3 \right)}^{2}}$, we get:
$\begin{align}
  & {{y}^{2}}+6y-2x+5+{{\left( -3 \right)}^{2}}-{{\left( -3 \right)}^{2}}=0 \\
 & \Rightarrow {{\left[ y-\left( -3 \right) \right]}^{2}}=2x-5+9 \\
 & \Rightarrow {{\left[ y-\left( -3 \right) \right]}^{2}}=2x+4 \\
 & \Rightarrow {{\left[ y-\left( -3 \right) \right]}^{2}}=2\left( x-\left( -2 \right) \right) \\
\end{align}$
Now, we know that the general equation of the parabola is as ${{\left( y-k \right)}^{2}}=4a\left( x-h \right)$ where (h, k) is the vertex.
So, by comparing the expression we got to the standard equation of parabola, we get:
$\left( h,k \right)=\left( -2,-3 \right)$ and $a=\dfrac{1}{2}$
So, the above conclusion proved that statement (I) is true.
Then, we also know that the equation of directrix of parabola is given by:
$x-h+a=0$
So, by substituting the value of h and a, we get:
$\begin{align}
  & x-\left( -2 \right)+\dfrac{1}{2}=0 \\
 & \Rightarrow x+2+\dfrac{1}{2}=0 \\
 & \Rightarrow \dfrac{2x+4+1}{2}=0 \\
 & \Rightarrow 2x+5=0 \\
\end{align}$
So, the equation of the directrix of parabola is $2x+5=0$ which is not matching the condition (II).
So, the above conclusion states that statement (II) is false.
Hence, option (b) is correct.

Note: Now, to solve these type of the questions we need to know some of the basic equations of the parabola as one of the given statement is y+3=0 which not the directrix equation but it is actually the equation of the axis which is in general given by:
$y-k=0$
Now, we know that the value of k is -3 so, we get y+3=0 which is actually the equation of the axis.